Arquímedes y el método de Exhausción

Arquímedes usó resultados de Euclides y Aristeo. Demostró teoremas sobre áreas y volúmenes por medio del método de exhausción, es decir, usando figuras líneas inscritas y circunscritas para llenar el área de un volumen. Sin embargo, también utilizó el método indirecto en algún momento de sus demostraciones. Es decir, no llegó a dar el salto hacia el concepto moderno de límite. Esto lo realiza en su libro Sobre la esfera y el cilindro. Debe mencionarse que el segundo libro de esta obra incluye resultados de álgebra geométrica

El método de Exhausción 

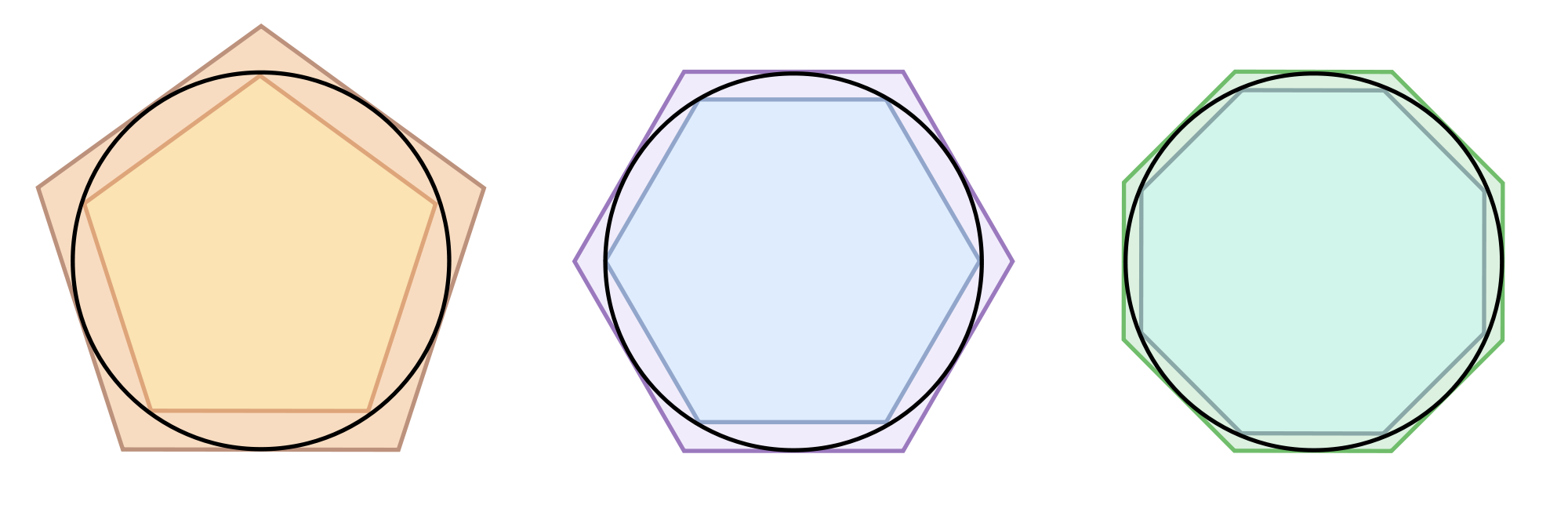
El método de Exhausción nace del problema de comparar las figuras curvilíneas y las rectilíneas. Como se sabe, uno de los grandes problemas de la Antigüedad era cómo reducir el círculo, o longitudes curvas, a segmentos de recta, y otro: cómo reducir cualquier línea curva a líneas rectas y círculos (esto se traduce como la construcción de figuras curvas usando solo regla y compás). No obstante, el "método de Exhausción'' no fue llamado así por los griegos, sería mucho tiempo después que Gregoire de St. Vincent (1 589 - 1 667) lo bautizaría de esa manera.

En ese escenario fueron usados dos principios generales sobre los números y sus relaciones con el infinito, que aparecieron de diferente forma, y fueron relevantes para la utilización del método que analizamos.

Primer principio:

"Cualquier cantidad, por más pequeña que sea, puede hacerse tan grande como se quiera multiplicándola por un número suficientemente grande''

Este se puede formular de la siguiente manera:

"Dadas dos magnitudes diferentes α y β (con β<α) existe entonces:

a) un número n tal que n β> α (esto se encuentra en el Libro V de los Elementos de Euclides, Def. 4)

b) un número n tal que n( α-β)> γ  donde γ es cualquier magnitud de la misma clase (esto se llama el Axioma de Arquímedes, en el trabajo Sobre la esfera y el cilindro de ArquímedesLibro I)''

Segundo principio:

"Si de cualquier magnitud sustraemos una parte no menor que su mitad, y si del resto sustraemos de nuevo una cantidad no menor que su mitad, y si continuamos repitiendo este proceso de sustracción, terminaremos por obtener como resto una magnitud menor que cualquier magnitud del mismo tipo dada de antemano''.

Lo anterior se puede poner también así:

"Dadas dos magnitudes diferentes α y β ( con β<α , existe un número n tal que (1-p)ⁿα< β , donde p≥ ½ (esto se encuentra en los Elementos de Euclides, Libro X, Def.

1)''.

Podemos ilustrar los principios usados por los griegos de la siguiente manera:

Tómese α=2000, β=2 y γ=8000

La primera forma del principio dice que se puede encontrar un n tal que βn≥ α

entonces: 
2n ≥ 2000

Se puede considerar n mayor que 1000 y ya funciona.
Veamos, si n=1500 entonces a
2x1500= 3000 ≥ 2000
La segunda forma del principio:
α-β=2000-2=1998


Se debe encontrar un n tal que



n x  (α-β) ≥ γ
Es decir, de tal manera que

nx1998 ≥ 8000
Este n=1500 sirve; pues

 1500x1998 ≥ 8000
 Veamos ahora el segundo principio:
Sea p=3/4,  y los mismos α y β de antes. Queremos encontrar un n tal que  
 (1-p)ⁿα≤ β 
 o que

(1-3/4)ⁿx2000≤ 2

Es decir:
(1/4)ⁿx2000≤ 2
Con n =5 obtenemos





(1/4)⁵x2000 = 0,000976563x2000 = 1,953125 
Y entonces:



1,9531125 ≤ 2