Su Vida:
 |
| La Haya, Holanda |
Descartes fue un gran intelectual en su tiempo. Un gran filósofo, físico y matemático, e incluso uno de los fundadores de la biología moderna.
Filósofo, Físico,
Matemático y pre-biologo.
 |
| Regulae ad Directionem Ingenii |
Descartes fue un gran
intelectual en su tiempo. Un gran filósofo, físico y
matemático, e incluso uno de los fundadores de la biología moderna.
Tuvo una importante influencia durante el siglo XVII. Sus dos
primeros libros fueron Regulae ad Directionem Ingenii ("Reglas
para la dirección de la mente'') en 1628, y Le Monde ("Sistema
del mundo'') en 1634. Esta primera obra publicada de manera
póstuma.
ofreció una prueba de la existencia de Dios a través de su método
Su relación con la
iglesia.
En cuanto a la segunda
obra, Descartes no la quizo publicar por temor a la persecución de
la Iglesia Católica. En ella
explicaba cómo los planetas giraban alrededor del Sol. Sin duda, la
obra más decisiva intelectualmente fue el Discours de la
méthode pour bien conduire sa raison, et chercher la vérité dans
les sciences ("Discurso del Método''), 1637, que
contiene 3 apéndices que no suelen incorporarse en las típicas
ediciones modernas del libro. Estos son: La Géométrie, La
Dioptrique y Les Méteores.
Descartes fue un
religioso devoto. De hecho, ofreció una prueba de la
existencia de Dios a través de su método. Sin embargo, la
Inquisición decidió castigar sus obras colocándolas en el Índice
de libros prohibidos poco tiempo después de su fallecimiento.
Llegó a la conclusión de que ese método era, en esencia, el de las matemáticas, o por lo menos lo que él pensaba que era el método de éstas.
El Método:
Descartes se colocó
en ruptura con los planteamientos escolásticos y medievales.
Trató de proponer un método diferente para el establecimiento del
conocimiento verdadero del mundo.
Llegó a la
conclusión de que ese método era, en esencia, el de las
matemáticas, o por lo menos lo que él pensaba que era el método de
éstas. Descartes establecía tres principios: en primer
lugar, la aceptación como cierto solamente de aquello que aparezca
en la mente como cierto y verdadero; en segundo lugar, que este
proceso ofrezca ideas básicas, claras y distintas y, en tercer
lugar, finalmente, que a partir de estas ideas y a través de la
deducción lógica es posible obtener el conocimiento verdadero.
Para Descartes existen
verdades innatas, claras y distintas. Para ello se basaba en un
"principio de la evidencia''. Formula la "duda metódica''
que exige una evidencia racional para el conocimiento. Usando este
método, Descartes concluye ciertas verdades. La primera es la
existencia propia, con su famoso "pienso luego existo''.
En segundo lugar, concluye la percepción del mundo exterior: el
mundo existe. En tercer término, es la comprensión de la estructura
matemática del mundo: la estructura de la realidad es matemática.
Claro, Descartes se pregunta si estas evidencias podrían ser el
resultado o la acción de un genio maléfico y es aquí,
precisamente, donde hace intervenir la existencia de Dios. La
existencia de Dios es el fundamento de sus evidencias racionales.
Para Descartes la esencia de la ciencia estaba constituida por las matemáticas
Las Matemáticas:
Para Descartes la esencia de la ciencia estaba
constituida por las matemáticas. La geometría, por ejemplo,
ofrecía primeros principios para deducir las propiedades del
espacio. Esto hacía Descartes al reducir la naturaleza de la materia
a las propiedades de forma, extensión y movimiento en el espacio y
el tiempo. Extensión y movimiento eran la clave. Precisamente, por
ser estas propiedades expresables matemáticamente, Descartes
afirmaba la naturaleza matemática de la realidad.
Dios creó el mundo bajo un diseño matemático
El sentido matemático,
sin embargo, tenía para Descartes un origen divino. Dios creó
el mundo bajo un diseño matemático. Si bien este gran
intelectual de todos los tiempos ayudó en la ruptura con el
pensamiento medieval escolástico y aristotélico, abriendo
posibilidades para el pensamiento libre y para el progreso de las
ciencias, también enfatizó la existencia de verdades a priori sin
recurrir a la experiencia sensorial práctica, es decir, verdades de
naturaleza metafísica.
Para Descartes, hay dos
dimensiones decisivas de las matemáticas: la axiomática y la
derivación lógica. Él pensaba que estas dimensiones podían
ser aplicadas en todas las áreas del conocimiento.
Descartes propuso una visión mecanicista en el conocimiento de la realidad
Ruptura con el
pensamiento medieval:
¿Y cómo se separaba del
pensamiento medieval y escolástico? La escolástica había
establecido un modelo de la realidad
organicista. A la par de esta metodología que enfatiza las
matemáticas, Descartes propuso una visión mecanicista en el
conocimiento de la realidad. Se trataba de entender que todos
los fenómenos de la naturaleza se podían describir a través de
leyes de la mecánica. Hay aquí, por supuesto, una influencia de los
hallazgos en mecánica y física de la época. Esta visión ha tenido
una gran influencia en la cultura y la ciencia occidentales hasta
nuestros días. Entonces: Descartes se oponía a la visión medieval
con un esquema mecanicista y matemático. Otro ejemplo: Descartes
afirmaba que la tierra y los astros eran de la misma naturaleza.
Más aun, afirmaba que el universo era indefinido e, incluso, pensaba
que eran posibles alteraciones momentáneas de la leyes de la
naturaleza. Esto era una confrontación directa con la visión
aristotélica y escolástica que establecía un mundo creado e
inmutable que se conservaba perpetuamente.
Por otra parte, para
Descartes los dominios de la ciencia y la fe debían ser separados
claramente. Los argumentos de la fe y la autoridad no podía formar
parte del razonamiento crítico y científico.
En esto, Descartes
convergía también con Kepler y Galileo.
Descartes promovió el método deductivo y el poder de la razón. En éste las matemáticas eran decisivas
Mientras que Bacon
enfatizó el papel de la experiencia empírica, Descartes
promovió el método deductivo y el poder de la razón. En éste las
matemáticas eran decisivas. En su visión mecanicista del
mundo, reducía el espacio a las categorías de extensión y
movimiento, dentro de una cosmología regulada por la leyes de la
mecánica, y buscaba reducir esta última precisamente a la
geometría. No puede olvidarse que Descartes es uno de los creadores
de la geometría de coordenadas, y de una visión de las matemáticas
que reafirmaba el papel del álgebra de una manera novedosa, a pesar de que
siempre consideraba a la geometría como la disciplina más
importante de las matemáticas.
La notación moderna de coordenadas dio fruto en la obra de Descartes
Su legado Matemático:
La notación
moderna de coordenadas dio fruto en la obra de Descartes. En
la vida cotidiana estamos familiarizados con espacio de dos y tres
dimensiones, y se necesita un gran esfuerzo de imaginación para
contemplar otras posibilidades. Nuetro sistema visual presenta a cada
ojo el mundo exterior como una imagen bidimensional (como la
pantalla del televisor). Imágenes ligeramentes diferentes
procedentes de cada ojo
se combinan en el cerebro para dar una sensación de profundidad,
gracias a la cual percibimos el mundo circundante como si tuviera
tres dimensiones.
Su idea es que la geometría del plano puede reinterpretarse en términos algebraicos.
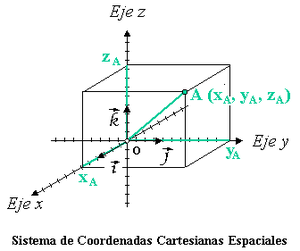
La clave para los
espacios multidimensionales es la idea de un sistema de coordenadas,
que fue introducido por Descartes por Descartes en un apéndice, “la
geometría”, a su “Discurso del método”. Su idea es que la
geometría del plano puede reinterpretarse en términos algebraicos.
Su enfoque es esencialmente el que ya se ha señalado. Escogemos un
punto en el plano y le llamamos el origen. Trazamos dos ejes: líneas
que pasan por el origen y se cortan a ángulos rectos. Etiquetamos un
eje con el símbolo x y el otro con el símbolo y. Entonces cualquier
punto P en el plano está determinado por el par de distancias(x,y),
que nos dice lo lejos que está en el punto del origen cuando se mide
paralelamente a los ejes x e y, respectivamente.
Por ejemplo, en un mapa x
podría ser la distancia al este del origen (los valores negati vos
representan distancias al oeste), mientras que y podría ser la
distancia al norte del origen (los valores negativos representan las
disntacias al sur). Las coordenadas funcionan también en un espacio
tridimensional, pero ahora dos números no son suficientes para
localizar un punto. Sin embargo, tres número sí lo son. Además de
las distancias este-oeste y norte-sur , necesitamos saber lo lejos
que esta un punto por encima o por debajo del origen. Normalmente
utilizamos un número positivo para distancias hacia arriba, y un
número negativo para distancias hacia abajo. Las coordenadas en el
espacio toman la forma (x,y,z).
Por
esto se dice que el plano es bidimensional, mientras que el espacio
es tridimensial. El número de dimensiones viene dado por cuántos
números necesitamos para especificar un punto.
Nótese
que la palabra “dimensión” no está definida aquí por si misma.
No encontramos el número de dimensiones de un espacio encontrando
algunas cosas llamadas dimensiones y contándolas luego. En su lugar,
calculamos cuántos números se necesitan para especificar una
posición en el espacio, y ése el número de dimensiones.













No hay comentarios:
Publicar un comentario