Podemos decir que las matemáticas en las civilizaciones primitivas, en gran medida, refieren al cálculo de terrenos, a la decoración en cerámica, al comercio más trivial, a los modelos y diseños en la ropa o al recuento del correr del tiempo en la vida cotidiana
Influjo empírico y práctico en los
orígenes de las matemáticas
Podemos decir que las
matemáticas en las civilizaciones primitivas, en gran medida,
refieren al cálculo de terrenos, a la decoración en cerámica, al
comercio más trivial, a los
modelos y diseños en la ropa o al
recuento del correr del tiempo en la vida cotidiana. Esto
no debe,
sin embargo, verse con malos ojos. Porque se trata de un sentido
íntimo de las
matemáticas, imbricadas en la práctica humana,
inmersas interactivamente en su
entorno.
En relación con las culturas orientales primitivas, señala Struik:
"La matemática Oriental se originó como una ciencia práctica para facilitar el cómputo del calendario, la administración de las cosechas, la organización de trabajos públicos, y la recolecta de impuestos. El énfasis inicial estaba naturalmente en la aritmética práctica y la medición. Sin embargo, una ciencia cultivada durante siglos por un oficio especial cuya tarea no sólo es aplicarlo sino también para instruir en sus secretos, desarrolla tendencias hacia la abstracción. Gradualmente, llegará a ser estudiada en sí misma. La aritmética no sólo evolucionó hacia el álgebra porque permitió cómputos prácticos mejores, pero también porque era el resultado natural de una ciencia cultivada y desarrollada en las escuelas de escribas. Por estas mismas razones, la medición se desarrolló hacia los principios -pero no más- de una geometría teórica.'' [Struik, A Concise History of Mathematics, p. 18]
Según la opinión de los historiadores, Egipto nace alrededor del año cuatro mil a.C. y su máximo esplendor se dio alrededor del año 2 500 a.C. Al igual que con Mesopotamia, la civilización siguió un curso que se vería drásticamente alterado solo hasta la conquista macedonia. Las principales referencias que tenemos en relación con las matemáticas egipcias son documentos escritos sobre papiro, un material frágil, por lo que realmente se tiene muy poca base para una descripción precisa de la naturaleza y los límites de la cultura y las matemáticas de esta civilización.
Uno de los papiros sobrevivientes es el llamado papiro de Moscú (se encuentra en el Museo de Bellas Artes de Moscú), otro el papiro Rhind -en honor de Henry Rhind- también llamado el papiro Ahmes, el nombre supuestamente del autor (este último en el Museo Británico). Se ha cifrado el año 1 650 a.C. para este último, y 1 850 a.C. para el primer papiro.
En relación con el primero, aparecen 87 problemas y sus soluciones, en el segundo 25.
Según la opinión de los historiadores, las matemáticas que aparecen en estos papiros ya eran conocidas por lo menos desde el año 3500 a.C. Struik hace la siguiente valoración sobre el carácter de estos problemas:
"Estos problemas ya eran erudición antigua cuando los manuscritos fueron compilados, pero hay papiros más pequeños de una fecha mucho más reciente incluso de los tiempos romanos, que no muestran ninguna diferencia en su aproximación. La matemática que ellos profesan es basada en un sistema decimal de numeración con signos especiales para cada unidad decimal mayor, un sistema con el que nosotros estamos familiarizados a través del sistema romano que sigue el mismo principio: MDCCCLXXVIII=1878. Sobre la base de este sistema los egipcios desarrollaron aritmética de un carácter predominantemente aditivo, que significa que su tendencia principal era reducir toda la multiplicación a las sumas repetidas. Por ejemplo, la multiplicación por 13 era obtenida multiplicando primero por 2, luego por 4, entonces por 8, y agregando los resultados de la multiplicación por 4 y 8 al número original.'' [Struik, D.: A Concise History of Mathematics, p. 20].
Es conocido el hecho de que la escritura egipcia era realizada por medio de los jeroglíficos, lo que también sucedía con los símbolos numéricos. Sin embargo, se puede considerar que usaron 3 sistemas de notación diferentes: jeroglífico, hierático y demótico. El primero mediante imágenes, el segundo simbólico, y el tercero una adaptación de la notación hierática. Se afirma que los dos primeros se usaron desde temprano en la historia egipcia, y precisamente el segundo aparece en los papiros mencionados. La última notación habría sido relevante en los periodos griego y romano de los egipcios.
La notación jeroglífica fue sustituida por la hierática.
Ahora bien, la multiplicación solo requería conocer la suma y la multiplicación por 2.
Otro detalle interesante es que, salvo en algunos casos, descomponían todas las fracciones en las llamadas fracciones unitarias. Por ejemplo, como
como 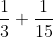 . En el papiro de Ahmes aparece una tabla con la descomposición de fracciones de la forma
. En el papiro de Ahmes aparece una tabla con la descomposición de fracciones de la forma 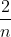 en fracciones de la unidad. Incluye, entre otros,
en fracciones de la unidad. Incluye, entre otros,
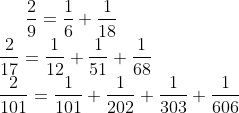
En relación con las culturas orientales primitivas, señala Struik:
"La matemática Oriental se originó como una ciencia práctica para facilitar el cómputo del calendario, la administración de las cosechas, la organización de trabajos públicos, y la recolecta de impuestos. El énfasis inicial estaba naturalmente en la aritmética práctica y la medición. Sin embargo, una ciencia cultivada durante siglos por un oficio especial cuya tarea no sólo es aplicarlo sino también para instruir en sus secretos, desarrolla tendencias hacia la abstracción. Gradualmente, llegará a ser estudiada en sí misma. La aritmética no sólo evolucionó hacia el álgebra porque permitió cómputos prácticos mejores, pero también porque era el resultado natural de una ciencia cultivada y desarrollada en las escuelas de escribas. Por estas mismas razones, la medición se desarrolló hacia los principios -pero no más- de una geometría teórica.'' [Struik, A Concise History of Mathematics, p. 18]
 |
| Escuela de Escribas |
Dos de las civilizaciones de la Edad del Bronce relevantes para la historia de las ciencias y las matemáticas, importantes nutrientes de las matemáticas griegas, fueron la egipcia y la babilónica
Muchas de las matemáticas
en las culturas orientales deben buscarse en esas
realizaciones
prácticas precisamente, para evaluar el conocimiento matemático de
que
disponían.
Dos de las civilizaciones
de la Edad del Bronce relevantes para la historia de las ciencias
y
las matemáticas, importantes nutrientes de las matemáticas griegas,
fueron la egipcia y
la babilónica, pueblos que ocuparon regiones
alrededor de importantes ríos:
respectivamente, alrededor del Nilo
y alrededor del Tigris y Éufrates. En el caso de estos
últimos, es
necesario decir que no se trataba de una sola civilización sino, más
bien, de
varios pueblos alrededor de las regiones mencionadas. A
pesar de ello, se considera que,
en relación con las matemáticas,
hubo cierta continuidad y una tradición desde los
tiempos más
remotos hasta la conquista de esos territorios por parte de los
macedonios.
Egipcios
La historia de las matemáticas en Egipto, aunque diferente de la de los babilonios, no trascendió los límites prácticos y la evidencia empírica en sus construcciones teóricas.Según la opinión de los historiadores, Egipto nace alrededor del año cuatro mil a.C. y su máximo esplendor se dio alrededor del año 2 500 a.C. Al igual que con Mesopotamia, la civilización siguió un curso que se vería drásticamente alterado solo hasta la conquista macedonia. Las principales referencias que tenemos en relación con las matemáticas egipcias son documentos escritos sobre papiro, un material frágil, por lo que realmente se tiene muy poca base para una descripción precisa de la naturaleza y los límites de la cultura y las matemáticas de esta civilización.
Uno de los papiros sobrevivientes es el llamado papiro de Moscú (se encuentra en el Museo de Bellas Artes de Moscú), otro el papiro Rhind -en honor de Henry Rhind- también llamado el papiro Ahmes, el nombre supuestamente del autor (este último en el Museo Británico). Se ha cifrado el año 1 650 a.C. para este último, y 1 850 a.C. para el primer papiro.
| Papiro de Moscú |
Sobre la base de este sistema los egipcios desarrollaron aritmética de un carácter predominantemente aditivo, que significa que su tendencia principal era reducir toda la multiplicación a las sumas repetidas
Según la opinión de los historiadores, las matemáticas que aparecen en estos papiros ya eran conocidas por lo menos desde el año 3500 a.C. Struik hace la siguiente valoración sobre el carácter de estos problemas:
"Estos problemas ya eran erudición antigua cuando los manuscritos fueron compilados, pero hay papiros más pequeños de una fecha mucho más reciente incluso de los tiempos romanos, que no muestran ninguna diferencia en su aproximación. La matemática que ellos profesan es basada en un sistema decimal de numeración con signos especiales para cada unidad decimal mayor, un sistema con el que nosotros estamos familiarizados a través del sistema romano que sigue el mismo principio: MDCCCLXXVIII=1878. Sobre la base de este sistema los egipcios desarrollaron aritmética de un carácter predominantemente aditivo, que significa que su tendencia principal era reducir toda la multiplicación a las sumas repetidas. Por ejemplo, la multiplicación por 13 era obtenida multiplicando primero por 2, luego por 4, entonces por 8, y agregando los resultados de la multiplicación por 4 y 8 al número original.'' [Struik, D.: A Concise History of Mathematics, p. 20].
| Numeración Egipcia |
Es conocido el hecho de que la escritura egipcia era realizada por medio de los jeroglíficos, lo que también sucedía con los símbolos numéricos. Sin embargo, se puede considerar que usaron 3 sistemas de notación diferentes: jeroglífico, hierático y demótico. El primero mediante imágenes, el segundo simbólico, y el tercero una adaptación de la notación hierática. Se afirma que los dos primeros se usaron desde temprano en la historia egipcia, y precisamente el segundo aparece en los papiros mencionados. La última notación habría sido relevante en los periodos griego y romano de los egipcios.
Los egipcios poseían una aritmética básicamente aditiva, es decir, por ejemplo, reducían la división y la multiplicación a sumas.Los egipcios poseían una aritmética básicamente aditiva, es decir, por ejemplo, reducían la división y la multiplicación a sumas. En la notación jeroglífica usaron símbolos específicos para las potencias de 10. En la hierática, también se usaba las potencias del 10, pero con menos símbolos.
La notación jeroglífica fue sustituida por la hierática.
Ahora bien, la multiplicación solo requería conocer la suma y la multiplicación por 2.
Otro detalle interesante es que, salvo en algunos casos, descomponían todas las fracciones en las llamadas fracciones unitarias. Por ejemplo,
A través de esta descomposición los egipcios realizaban operaciones aritméticas con todas las fracciones, en particular multiplicaciones y divisiones. Sin embargo, era un proceso complicado.
Para dividir usaban un método parecido al del mínimo común denominador.
Por otro lado, se piensa que tampoco tuvieron mucha conciencia sobre la naturaleza de los números irracionales.
El método de las fracciones de la unidad permitía ciertas aplicaciones prácticas. En el papiro de Ahmes, en relación con la distribución de panes y al pago a los empleados de un templo.
Los papiros mencionados contenían algo similar a lo que son las ecuaciones lineales en una incógnita. El problema 72 del papiro de Ahmes es: Si tenemos que intercambiar 100 panes de pesu 10 por un determinado número de panes de pesu 45, ¿cuál es este número determinado?
Pesu = Nº panes o jarras / heqats de grano
Al igual que con los babilonios encontramos progresiones aritméticas y geométricas.
Sin embargo, no usaron mucho simbolismo.la geometría, la opinión más generalizada es que la usaban, al igual que los babilonios, como un instrumento para resolver problemas prácticos.
En relación con la geometría, la opinión más
generalizada es que la usaban, al igual que los babilonios, como un
instrumento para resolver problemas prácticos. La aritmética y la
geometría no aparecían separadas; más bien, lo que se daba era una
aplicación de álgebra y aritmética a problemas relacionados con
figuras geométricas que emergían en situaciones del entorno.
Aparecen tripletes pitagóricos, por lo que alguna
familiaridad debían tener con el teorema de
Pitágoras.
Mucho de lo que hicieron los egipcios en matemáticas
está vinculado a transacciones comerciales,
edificaciones, cálculo
de superficies, medidas de terrenos, y a diversos asuntos de
naturaleza
práctica en sociedades asentadas básicamente en la
agricultura.
En relación con la astronomía, la opinión es que
su nivel estaba por debajo de los babilonios. No
obstante, se
reconoce que los egipcios lograron una determinación del año y un
calendario bastante
útiles. Lo que sí llama la atención es una
combinación de astronomía y geometría para la
edificación de
templos que son hasta nuestros días un símbolo emblemático de esta
civilización: las
pirámides.










Este comentario ha sido eliminado por el autor.
ResponderEliminar