Leibniz nació en Leipzig y vivió casi siempre alrededor de Hanover, Alemania, donde trabajó para
los duques (uno de ellos fue Rey de Inglaterra con el nombre de Jorge I). Estudió derecho e hizo su
primera tesis en lógica.
| Actual Leipzig |
En 1666, escribió su
tesis doctoral De Arte Combinatoria ("Sobre el arte de las
combinaciones''), en la que formuló un método
universal para razonar.
Se trataba de un hombre
de grandes cualidades intelectuales que además de matemático, fue
filósofo, abogado, filólogo, historiador e incluso hizo aportes a
la geología. Aunque sus
contribuciones no llegan al nivel de las de
Newton, hizo contribuciones en mecánica, óptica, hidrostática,
neumática, ciencia náutica, en la lógica y hasta en la
construcción de máquinas calculadoras. Se ganó la vida como
diplomático y abogado, pero sus trabajos en las matemáticas y
la
filosofía fueron muy relevantes.
| Calculadora de Leibniz |
Se dice que siempre trató
de conciliar las religiones católica y protestante. También fue un
promotor de sociedades académicas con el propósito de promover las
ciencias y las técnicas en
reacción al carácter conservador y
retrógrado de las universidades de su tiempo. Al igual que
Galileo,
escribió en lengua vernácula, privilegió el alemán frente al
latín.
Leibniz propuso un método
universal para conocer, crear y entender la profunda unidad
del
universo: la scientia generalis. Y también la creación de un
lenguaje perfecto para realizar el
razonamiento por medio de
cómputos simples: la lingua characterica.
Estos proyectos motivaron
parte de su trabajo intelectual, y le condujeron en el primer caso
a
resultados matemáticos, y en el segundo a ofrecer aportes en la
lógica y en la simbología
matemáticas.
Es interesante que
Leibniz fue influenciado por Descartes de una manera particular. Este
último
tuvo una influencia importante en los matemáticos
holandeses; debe recordarse que pasó unos
veinte años en Holanda.
Tuvo influencia en particular sobre Frans van Schooten (1615 –
1660)
quien propagó y amplió la geometría analítica cartesiana,
e incluso hizo una versión en latín de la
Géométrie. Huygens fue
uno de los discípulos de van Schooten, un gran científico con
aportes en la
teoría de la luz, en astronomía y al que se le
atribuye el reloj de péndulo. En 1666, Huygens se
trasladó a París,
en donde permaneció hasta 1681. Este matemático, ya en 1656, había
aplicado
métodos infinitesimales a las cónicas (por ejemplo, redujo
la "rectificación'' de la parábola a la
"cuadratura'' de
la hipérbola).
 |
| Frans van Schooten |
Leibniz estuvo en París,
al parecer, entre los años 1673 y 1676. Por influencia directa de
Huygens
estudió los trabajos de Descartes, Pascal y algunos
matemáticos británicos. La relación entre
Leibniz y Huygens fue
importante para el trabajo de Leibniz en el cálculo. Es posible ver
la
relación entre estos dos matemáticos en el desarrollo conjunto
del concepto de energía cinética.
Se debe mencionar que
Leibniz sabía del rumor de que Newton ya manejaba un nuevo método,
y esto contribuyó a
estimular su trabajo.
Mientras el enfoque de
Newton fue físico, el de Leibniz fue esencialmentegeométrico,
incluso algebraico o lógico.
Desde que Leibniz entró
en contacto con las matemáticas, bajo la influencia de Huygens, le
dio
importancia al cálculo de las tangentes a las curvas y, muy
rápidamente, estuvo seguro de que se
trataba de un método inverso
al de encontrar las áreas y volúmenes a través de sumas. Leibniz
escribió varios artículos entre 1675 y 1684 que expresan su
evolución en la construcción del
cálculo. En noviembre de 1676
ofreció las reglas
dxn=
ndxn-1 para un entero o fraccional y, también
En julio de 1677 Leibniz
ofrecía las reglas correctas para la diferencial de la suma,
diferencia, producto y cociente de 2 funciones y para potencias y
raíces, aunque no ofrecía pruebas.
Su método se recoge por
primera vez en un artículo que apareció en la revista Acta
eruditorum en 1684, que él mismo había fundado dos años antes
(donde ya había anunciado su método): Nova methodus pro maximis et
minimis, itemque tangentibus, quae nec fractas nec irrationales
quantitates moratur, et singulare pro illis calculi genus ("Un
nuevo método para máximos y mínimos, y también para tangentes,
que no se ve obstruido por las cantidades fraccionarias ni por las
irracionales'').
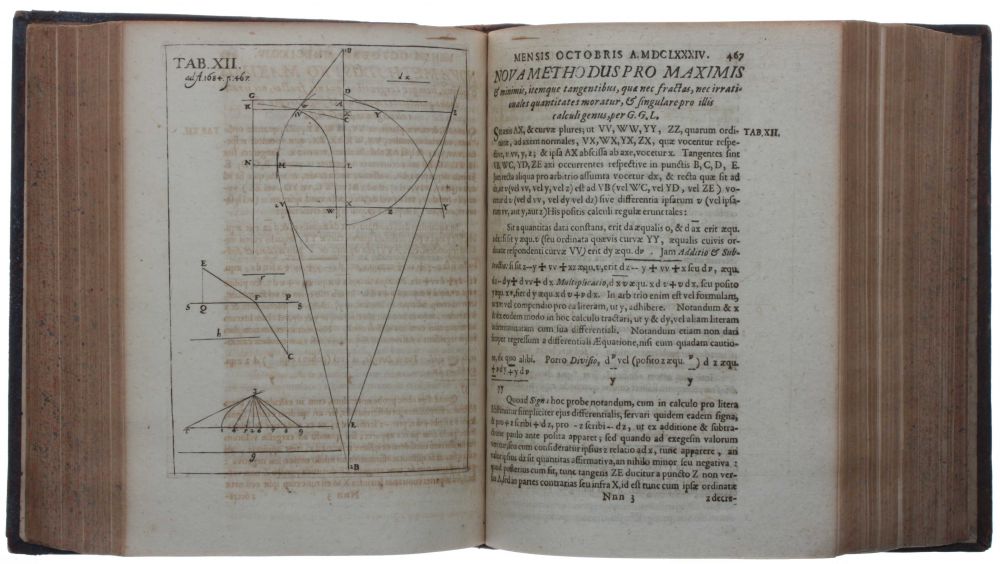 |
| Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationales quantitates moratur, et singulare pro illis calculi genus |
Se trataba de una
aproximación geométrica y no cinemática como en Newton. Se percibe
la influencia de Pascal y de Barrow (especialmente Geometrical
Lectures, 1670), así como de Huygens y Descartes. Ya aquí aparecían
las reglas básicas de la derivación, las condiciones para valores
extremos (máximos y mínimos) y para los puntos de inflexión.
Este artículo contenía, entonces, los símbolos dx, dy y las reglas
dy=0 para valores extremos relativos o d2y=0 para los puntos de inflexión.
dy=0 para valores extremos relativos o d2y=0 para los puntos de inflexión.
Fue Leibniz quien introdujo precisamente aquí el término "cálculo diferencial'' (de di-fe-ren-cias).
Aunque y se toman como funciones de , el término "función'' no aparece en este artículo. Este término aparecerá hasta 1692 en otro artículo.
Antes de usar "cálculo diferencial'' había usado la expresión "methodus tangentium directa''. También "methodus tangentium inversa'' o "calculus summatorius'' para la integración definida y, en 1698, "calculus integralis'' (específicamente, en un artículo con Jean Bernoulli).
Fue en el año 1686 cuando Leibniz hizo una publicación sobre la integración donde recogía el símbolo "∫''. No obstante, ya había utilizado otros símbolos para la noción de integral: primero omn. y (todas las y), luego ∫y y luego ∫ydx.
Aunque y se toman como funciones de , el término "función'' no aparece en este artículo. Este término aparecerá hasta 1692 en otro artículo.
Antes de usar "cálculo diferencial'' había usado la expresión "methodus tangentium directa''. También "methodus tangentium inversa'' o "calculus summatorius'' para la integración definida y, en 1698, "calculus integralis'' (específicamente, en un artículo con Jean Bernoulli).
Fue en el año 1686 cuando Leibniz hizo una publicación sobre la integración donde recogía el símbolo "∫''. No obstante, ya había utilizado otros símbolos para la noción de integral: primero omn. y (todas las y), luego ∫y y luego ∫ydx.
En 1675, usó la siguiente notación:
omn. => quería decir suma (del latín omnia),
l => significa dy
l => significa dy
Por ejemplo, omn.l = y queria decir en nuestra notación ∫dy=y y
Para Leibniz: dy y dx representaban cantidades arbitrariamente pequeñas (diferenciales o infinitesimales), y con ellas iría construyendo tanto su cálculo integral (sumas) como su cálculo diferencial (cálculo de tangentes). Los símbolos
Los trabajos de Leibniz
tuvieron una gran repercusión y potenciaron un desarrollo muy rápido
del
cálculo con su enfoque. En muy poco tiempo, por ejemplo, y con
la contribución relevante de los
hermanos Bernoulli, se puede decir
que se tenían los resultados básicos de lo que hoy se enseña en
los cursos de cálculo universitario.
Posteriormente, Euler y
otros matemáticos de la Europa continental darían continuidad a
esta obra.
Debe decirse que el enfoque de Newton, por medio de su
teoría de fluxiones, tuvo un desarrollo
más limitado con Taylor,
Maclaurin y otros matemáticos británicos. Ya volveremos sobre
esto.
Los símbolos
“=” y
“x”
serían aceptados de manera dominante debido a su
influencia. Los
términos de función y coordenadas también son
resultado de
la labor de Leibniz.
Leibniz al igual que
Newton también fue atacado por otros intelectuales de la época. El
médico y geómetra Bernard
Nieuwentijdt (1654 - 1718) en 1694 señalaba que había oscuridad en
el trabajo de Leibniz y que no podía
entender cómo diferían las "cantidades infinitamente
pequeñas'' de 0, y preguntaba cómo una suma
de infinitesimales podía dar algo finito.
 |
| Bernard Nieuwentijdt |
Debe decirse que ni
Leibniz ni Newton pudieron ofrecer una gran precisión y mucha
claridad
lógica en los fundamentos de sus métodos en el cálculo
diferencial e integral. Para ellos lo decisivo
era la coherencia en
sus resultados y la fecundidad de los nuevos procedimientos. Eso era
suficiente
para generar el progreso de esta nueva disciplina
matemática.
La motivación
fundamental de Leibniz por un método universal para obtener
conocimiento,
invenciones y mostrar o entender la unidad del mundo,
la búsqueda por una ciencia general, una
caracteristica generalis,
lo colocó en la trayectoria del descubrimiento del cálculo.
La influencia de Leibniz
sobre sus contemporáneos es directa. Por ejemplo, los hermanos
Bernoulli
realizaron un gran desarrollo de estos métodos. Un texto
de cálculo apareció en el año 1696,
titulado Analyse des
infiniment petits, escrito por el marqués de L'Hôpital, que incluyó
muchos
resultados de Johann Bernoulli.
Algo relevante en Leibniz
son sus contribuciones a la notación matemática. Influido por esa
otra
gran pretensión, aparte de una ciencia general, la creación
de una lengua universal que impidiera
los errores de pensamiento y
redujera éste al cómputo, la lingua universalis, este brillante
pensador
dejó una herencia extraordinaria en la simbología de las
matemáticas. Incluso, lo que ya
mencionamos, el nombre de cálculo
diferencial y cálculo integral encuentran su origen en él.
Aunque
se le atribuye su nombre a Leibniz las siguientes series fueron
desarrolladas por James
Gregory, quien contribuyó mucho al manejo
de los procesos que lidiaban con el infinito:


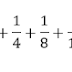






No hay comentarios:
Publicar un comentario