Kerala es un territorio
en el suroeste de la India. En la década de 1.940, investigadores
hindúes, con
Rajagopal al frente, retomaron un artículo escrito en
1835 por Charles Whish, en el que se afirma
la existencia de
importantes resultados en las matemáticas de Kerala, que formaron
toda una
escuela. Cuatro obras señalaba Whish que eran las claves
para la astronomía y las matemáticas:
Tantra Samgraha
(Nilakantha), Yuktibhasa (Jyesthadeva), Karana Paddhati (Putumana
Somayaji) y
Sadratnamala (Sankara Varman).
 |
| Tantra Samgraha |
Estas obras incluían,
según Whish, cálculo infinitesimal, series de Gregory y Leibniz
para  la
tangente inversa, series de potencias de Leibniz para
la
tangente inversa, series de potencias de Leibniz para  y la
de Newton para el seno y el coseno
(atribuidas a Madhava). Además,
aproximaciones racionales a funciones trigonométricas: la serie
de
Taylor, entre ellas. Estos últimos resultados obtenidos sin usar el
cálculo infinitesimal.
y la
de Newton para el seno y el coseno
(atribuidas a Madhava). Además,
aproximaciones racionales a funciones trigonométricas: la serie
de
Taylor, entre ellas. Estos últimos resultados obtenidos sin usar el
cálculo infinitesimal.
(AC+BD)}{AD+BC}}&space;&&space;y&space;&&space;Y=&space;\sqrt{\frac{(AD+BC)(AC+BD)}{AB+CD}}&space;\end{matrix})
Por medio de estos cuadriláteros cíclicos, la escuela de Kerala encontró las relaciones:
Por otra parte, tanto Aryabhata I y Brahmagupta introdujeron el concepto de movimiento instantáneo. Usaron, por ejemplo, la fórmula:
donde u,v y w son la longitud verdadera, media y anomalía media en un momento,u', v' y w' las mismas cantidades después de un momento,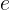 es la excentricidad de la máxima ecuación de la órbita.
es la excentricidad de la máxima ecuación de la órbita.
Manjula (930 d.C.) y Bhaskara ampliaron estos resultados. Este último obtuvo lo que se puede decir era:
Estos trabajos fueron ampliados por la escuela de Kerala.
Con estos elementos podemos afirmar que las matemáticas hindúes tuvieron un desarrollo considerable, en algunos casos adelantándose en siglos a los europeos. Sin embargo, todavía no están claras todas las conexiones y puentes entre hindúes y europeos. Pero hay una que sabemos que fue decisiva: los árabes.
 | |
| Serie de Leibniz |
Las series infinitas de  , al parecer,
estaban asociadas a la astronomía. Igual con los desarrollos para
las funciones trigonométricas. Es decir: para obtener tablas cada
vez más precisas para utilizar en los cálculos astronómicos. Tal
era la precisión que Madhava obtuvo valores correctos hasta la
posición decimal 8 o 9. Esto sería obtenido por los europeos 200
años después. Para algunos autores recientes, sus trabajos podrían
considerarlo el fundador del análisis matemático.
, al parecer,
estaban asociadas a la astronomía. Igual con los desarrollos para
las funciones trigonométricas. Es decir: para obtener tablas cada
vez más precisas para utilizar en los cálculos astronómicos. Tal
era la precisión que Madhava obtuvo valores correctos hasta la
posición decimal 8 o 9. Esto sería obtenido por los europeos 200
años después. Para algunos autores recientes, sus trabajos podrían
considerarlo el fundador del análisis matemático.
En la India existen otros temas
matemáticos de interés. Por ejemplo, el estudio de series
aritméticas por medio de diagramas. Esta
aproximación geométrica permitía ofrecer cierto grado de
convencimiento de los resultados.
También hicieron trabajos con
cuadriláteros inscritos en círculos (cuadrilátero cíclico). Ya
Brahmagupta había ofrecido algunos resultados. Consideremos la
siguiente figura.
Por medio de estos cuadriláteros cíclicos, la escuela de Kerala encontró las relaciones:
Por otra parte, tanto Aryabhata I y Brahmagupta introdujeron el concepto de movimiento instantáneo. Usaron, por ejemplo, la fórmula:
donde u,v y w son la longitud verdadera, media y anomalía media en un momento,u', v' y w' las mismas cantidades después de un momento,
Manjula (930 d.C.) y Bhaskara ampliaron estos resultados. Este último obtuvo lo que se puede decir era:
Estos trabajos fueron ampliados por la escuela de Kerala.
Con estos elementos podemos afirmar que las matemáticas hindúes tuvieron un desarrollo considerable, en algunos casos adelantándose en siglos a los europeos. Sin embargo, todavía no están claras todas las conexiones y puentes entre hindúes y europeos. Pero hay una que sabemos que fue decisiva: los árabes.










No hay comentarios:
Publicar un comentario