Arquímedes de Siracusa(287 a.C-212a.C)

Se considera el matemático más brillante de toda la Antigüedad

Nació en Siracusa, en la Magna Grecia(la Actual Sicilia), en el 287 a.C. y murió en el 212 a.C..Hijo del astrónomo Fidias. Visito Egipto, donde supuestamente inventó el tornillo de Arquímedes, que hasta hace poco era ampliamente utilizado para elevar agua del Nilo para irrigacipon. Es probable que visitara a Euclides en Alejandría, y seguro que mantuvo correspondencia con matemáticos alejandrinos.

Actual Siracusa

Se considera el matemático más brillante de toda la Antigüedad. Recibió su educación en Alejandría. Se afirma con toda justicia que el trabajo geométrico de Arquímedes fue el punto máximo de la matemática alejandrina.

 

Arquímedes usó resultados de Euclides y Aristeo. Demostró teoremas sobre áreas y volúmenes por medio del método de exhausción, es decir, usando figuras líneas inscritas y circunscritas para llenar el área de un volumen. Sin embargo, también utilizó el método indirecto en algún momento de sus demostraciones. Es decir, no llegó a dar el salto hacia el concepto moderno de límite. Esto lo realiza en su libro Sobre la esfera y el cilindro. Debe mencionarse que el segundo libro de esta obra incluye resultados de álgebra geométrica.

Principio de arquímedes: un cuerpo al sumerguirse en el agua, el agua ejerce sobre ese cuerpo una presión vertical de abajo hacia arriba que es igual al peso del agua desplazada

Es famoso en muchos campos. Se conoce muy bien el principio que lleva su nombre y que afirma que al sumergirse un cuerpo en el agua, el agua ejerce sobre ese cuerpo una presión vertical de abajo hacia arriba que es igual al peso del agua desplazada. Se dice que aquí empezó la hidrostática.

Arquímedes realizó importantes estudios sobre palancas. 

Apoyo Bélico

Sus habilidades matemáticas fueron insuperables y de amplio alcance. Les dio un uso práctico y construyó enorme máquinas de guerras basadas en su ley de la palanca, capaces de lanzar rocas enormes contra el enemigo. Sus máquinas fueron utilizadas con gran efecto en el sitio romano de Alejandría en el 212 a.C. Utilizó incluso la geometría de la reflexión óptima para concentrar los rayos solares sobre una flota romana e incendiar las naves.

Arquímedes será siempre recordado por su obra sobre círculos, esferas y cilindros

Legado Matemático:

Hizo importantes contribuciones a la geometría, estuvo en la vanguardia de las aplicaciones de las matemáticas al mundo natural y fue un ingeniero consumado. Pero para los matemáticos, Arquímedes será siempre recordado por su obra sobre círculos, esferas y cilindros, que ahora asociamos con el número Π. Por supuesto, los griegos no trabajaban directamente con Π; ellos lo veían geométricamente como la razón entre la circunferencia de un círculo y su diámetro.

Lambert

Culturas anteriores habían advertido que la circunferencia de un círculo es siempre el mismo múltiplo de su diámetro, y sabían que este múltiplo era aproximadamente 3 ½, quizá un poco mayor. Los babilonios utilizaban 3 ⅛. Pero Arquímedes fue mucho más lejos; sus resultados iban acompañados de demostraciones rigurosas, en el espíritu de Eudoxo. Hasta donde sabían los griegos, la razón entre la circunferencia de un círculo y su diámetro podría ser irracional. Ahora sabemos que realmente es así, pero la demostración tuvo que esperar hasta 1770, cuando Johann Heinrich Lambert

ideó una.

La geometría griega trabajaba mejor con polígonos: formas hechas de líneas rectas. Pero un círculo es curvo, de modo que Arquímedes se acercó al mismo aproximándolo por polígonos. Para estimar Π, él comparó la circunferencia de un círculo con los perímetro de dos series de polígonos: una serie situada en el interior del círculo, y la otra a su alrededor. Los perímetros de los polígonos dentro del círculo deben ser más cortos que el círculo, mientras que los de fuera del círculo deben ser más largos que el círculo. Para hacer el cálculo más fácil, Arquímedes construía sus polígonos bisecando repetidamente: los lados de un hexágono regular para obtener poligonos regulares con 12 lados, 24, 48 y asi sucesivamente. Se detuvo en 96. Sus cálculos demostraban que:

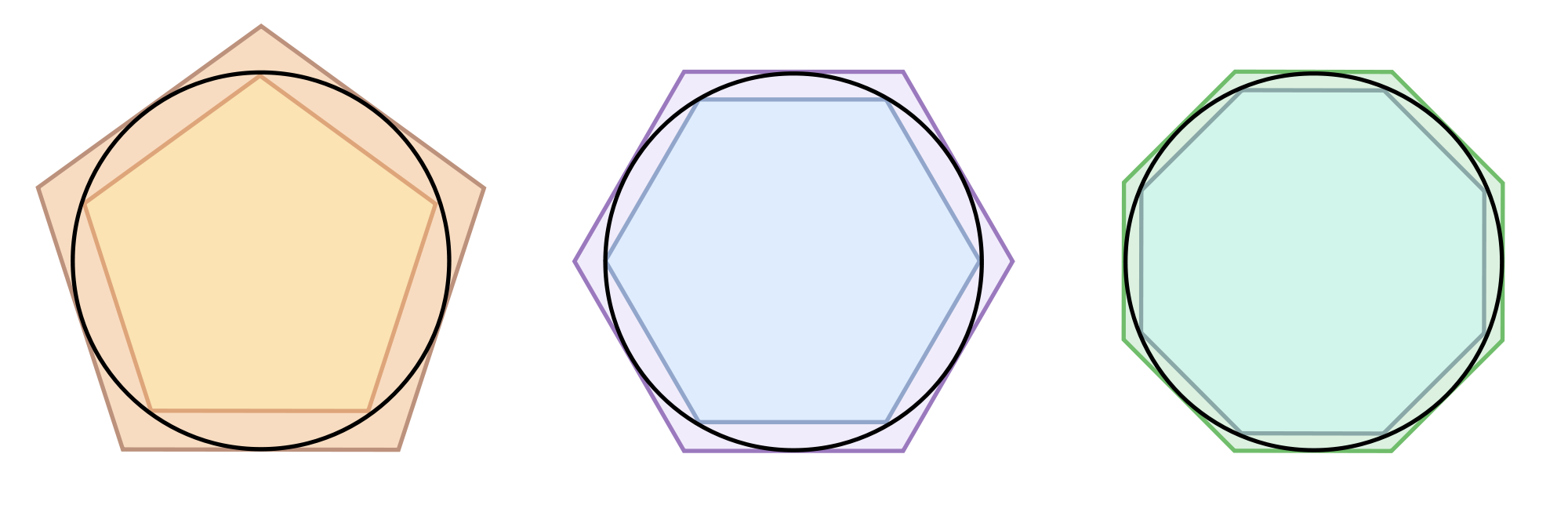Los perímetros de los polígonos dentro del círculo deben ser más cortos que el círculo, mientras que los de fuera del círculo deben ser más largos que el círculo

La obra de arquímedes sobre la esfera es de especial interés, porque no sólo conocemos su demostración rigurosa sino la forma en que la encontró. La demostración se da en su libro sobre la esfera y el cilindro circunscrito, y que las áreas de aquellas partes de la esfera y del cilindro que yacen entre dos planos paralelos cualquiera son iguales. En Lenguaje moderno, Arquímedes demostró que el volumen de una esfera es 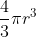, donde r es el radio, y el área de su superficie es 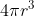. Estos hechos se siguen utilizando hoy.

La demostración hace un uso de la exhausción. Este método tiene una limitación importante: hay que saber cuál es la respuesta antes de tener muchas posibilidades de demostrarla. Durante siglos los estudiosos no tenían ninguna idea de cómo Arquímedes conjeturó la respuesta. Pero en 1906 el estudioso danés Heiberg estaba estudiando un pergamio del siglo XII en el que había escritas unas oraciones. Él advirtió líneas tenues de una inscripción anterior que había sido borrada para dejar lugar para las oraciones. Descubrií que el documento original era una copia de varias obras de Arquímedes, algunas de ellas previamente desconocidas. Una obra de Arquímedes, el Método de los teoremas mecánicos, explica cómo conjeturar el volumen de una esfera. La idea consiste en hacer rebanadas infinitamente delgadas de la esfera y colocar las rabanadas en un plato de una balanza; en el otro plato se cuelgan rebanadas similares de un cilindro y un cono, cuyos volúmenes Arquímedes ya conocía, La ley de la palanca da el valor buscado para el volumen.