Matemáticas védicas | La sección áurea | Sulbasutras

Entre el 1500 y el 800 a.C. se habla del periodo de las matemáticas védicas. Los Vedas eran colecciones de literatura en las que, entre muchas otras cosas, se encuentra matemática. Esto, en particular, en unos "apéndices'' llamados Vedangas. Entre ellos, los Sulbasutras trataban de construcción y medidas de altares sacrificiales, y aquí había geometría. 

Geometría de los Sulbasutras

Hubo 3 de ellos relevantes para las matemáticas, escritos, respectivamente, por: Baudhayana, Apastamba y Katyayana. El primero formula el teorema de Pitágoras, da un procedimiento para calcular la correcta hasta la quinta cifra decimal, y diversas construcciones geométricas. El segundo amplía estos temas. El último no añade mucho. La geometría aquí provenía de la integración de orientación, forma y área de los altares, según las prescripciones de los libros sagrados védicos. Había resultados geométricos, procedimientos de construcción de altares y algoritmos. El teorema de Pitágoras está incluido de la siguiente manera, por ejemplo, por Katyayana:

"La soga (estirada a lo largo de la longitud) de la diagonal de un rectángulo produce un (área) que producen conjuntamente los lados horizontal y vertical''.

En la construcción de un altar aparecen varios tripletes pitagóricos, incluso con números irracionales.

En las construcciones geométricas que planteaban, había cuadrados, rectángulos, trapecios y círculos, que se debían construir con restricciones de área. Un par de ejemplos: "Fusionar dos cuadrados iguales o desiguales para obtener un tercer cuadrado'', "transformar un rectángulo en un cuadrado de la misma área''. 

Las matemáticas védicas incluyen aproximaciones a raíces cuadradas. Se presume que esto se originó al intentar resolver el problema de construir un altar cuadrado que tuviera como área el doble de un cuadrado dado. Tanto Apastamba como Katyayana dieron soluciones. La aproximación fue 1,4142156, mientras, el valor real es 1,414213. ¡Nada mal! Los textos incluyen una fórmula que da la aproximación: 

Un comentarista de estos textos, del siglo XV, añadió 2 términos a esta serie, dando una aproximación con 7 dígitos correctos en la notación decimal; la serie quedaba así:

Hay un hecho curioso que se cita en un himno del Atharavaeda, en una figura que se usaba en las meditaciones, que estaba constituida por 6 triángulos isósceles, que generan a su vez 43 triángulos subalternos. La figura se llama: Sriyantra, algo así como gran "objeto''. Tomada de [George Gheverghese Joseph: La cresta del pavo real]. 

Sriyantra

Se trata de un problema de construcción geométrica bastante difícil. Pero lo más interesante, incluso sorprendente, es que el triángulo más grande de la figura constituye esencialmente una representación de una de las caras tringulares de la famosa pirámide de Gizeh en Egipto. Y conserva una de las razones más interesantes entre dos números-longitudes (irracionales) en la historia de las matemáticas: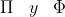. Este último número es la llamada razón áurea. Esta es, con exactitud, 1,61803, pero de manera fraccionaria es: es un número especial.

Una de las cosas interesantes es que emerge en los números de Fibonacci:

 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...

Cuando se avanza en la sucesión, la razón entre dos términos consecutivos 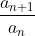 crecientemente a 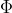. Por ejemplo, 233/144 da el valor que se tiene en la gran pirámide de Gizeh.

Antes de seguir, hagamos una pequeña digresión para ilustrar ese importante número que aparece por doquier en las matemáticas y la ingeniería; tanto que Kepler la llamó la "proporción divina''.

La sección áurea

Una forma de obtenerla es en los pentágonos regulares. Véase el siguiente procedimiento.

Tomemos el pentágono regular
ABCDE

y tracemos las 5 diagonales de éste.
Aquí obtenemos otro pentágono regular A'B'C'D'E'

Y, observe: A',B',C',D',E'  divide la diagonal correspondiente en 2 segmentos.

El resultado:

"La razón de la diagonal al segmento más largo es igual a la razón del mismo segmento al segmento más pequeño''.

En la figura siguiente, se tiene que:

También:

Sea d la diagonal y x el segmento mayor ().

La razón se puede escribir como

 lo que hoy en día decimos que es una ecuación de segundo grado:

Seguimos. En los Sulbasutras se puede apreciar un sistema de numeración posicional y decimal, aunque los datos detallados y transparentes aparecen en el trabajo de un astrónomo de mitad del 587 d.C.: Varahamihira.