Las Matemáticas en Alemania | siglo XIX | Weierstrass

Karl Weierstrass fue profesor de la Universidad de Berlín, aunque había sido maestro en una escuela secundaria durante muchos años. Especialmente durante este período que trabajó en secundaria escribió varios artículos sobre integrales hiperelípticas y sobre ecuaciones diferenciales algebraicas. Contribuyó notablemente a fundamentar la teoría de las funciones complejas sobre series de potencias.

Una de sus contribuciones fue el llamado principio de prolongación analítica. Pudo entonces definir una función analítica como una serie de potencias junto a todas aquellas obtenidas por medio de la prolongación analítica. Esto era útil por ejemplo en la solución de ecuaciones diferenciales en física matemática.

Brindó una gran atención a establecer rigor en la teoría de funciones y en el cálculo de variaciones.

Por ejemplo, en lo que se refiere a nociones de mínimo de una función, derivada, continuidad, etc. Fue Weierstrass precisamente quien descubrió la convergencia uniforme (por lo menos desde 1842): un asunto decisivo para poder diferenciar o integrar series término a término.

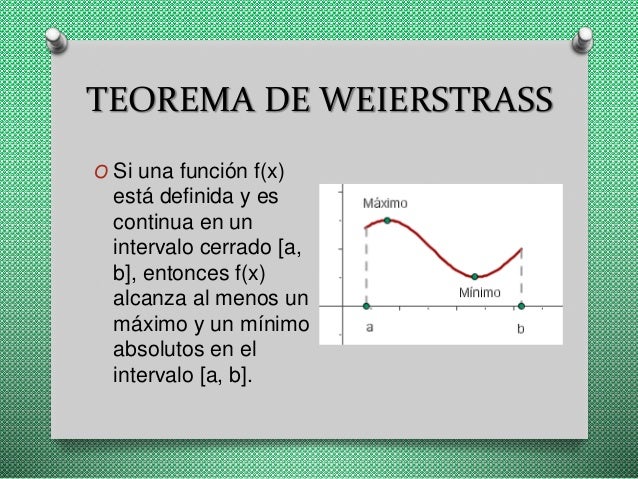
Weierstrass descubrió que una función continua sobre un intervalo cerrado sobre el eje real puede expresarse en ese intervalo como una serie de polinomios absoluta y uniformemente convergente. También incluyó funciones de varias variables.