Las Matemáticas del Renacimiento | Parte 4 | Aritmética y álgebra

A principios del siglo XVI, el cero y los irracionales se aceptaban, más o menos en la tradición de los árabes e hindúes. Cardano, Stevin, Pacioli y el alemán Michael Stifel introdujeron nuevos tipos de irracionales. Vieta dio una aproximación del número usando otras formas de irracionales. Stifel en su obra Aritmética Integra de 1 544 usó irracionales en forma decimal, aunque tenía sus dudas acerca de la naturaleza de los mismos, a los que no consideraba exactamente números de verdad.

Las dudas sobre los irracionales siguieron por siglos. Pascal y Barrow opinaron que números como la eran simplemente magnitudes geométricas, o sea eran símbolos sin existencia independiente más allá de esas magnitudes, y acudían a la teoría de las magnitudes de Eudoxo para justificar la operación con ellos. Stevin, por el contrario, afirmaba que los irracionales eran números independientes, e incluso los aproximó por medio de números racionales. En la misma dirección, John Wallis y Descartes llegarían a afirmar que los irracionales eran números.

Un tanto similar ocurría con los números negativos. En los siglos XVI y XVII matemáticos como el mismo Stifel afirmaron que eran números absurdos. Cardano obtuvo números negativos en algunas ecuaciones, pero no los consideraba números; es más, afirmaba que eran absurdos, ficticios. Vieta los descartó completamente. Pascal consideraba un sin sentido restar 4 al 0. Descartes sí los aceptó, aunque solo en parte (a las raíces negativas las llamaba falsas).

En la solución de ecuaciones cuadráticas y al usar la raíz cuadrada los matemáticos de la época se toparon con otros números aun más problemáticos: los complejos. Por ejemplo, Cardano al resolver la ecuación x(10-x)=40 encontró raíces complejas.

Algo similar ocurrió con Bombelli quien incluso llegó a formular las cuatro operaciones con los complejos en la forma actual. Pero tanto Cardano como Bombelli consideraban que se trataba de algo sin utilidad y de naturaleza sofística.

Aunque no tuvo mucha influencia en su tiempo, Albert Girard le dio valor a los complejos como soluciones formales de ecuaciones.

Descartes, a pesar de la gran amplitud de miras que siempre exhibía, rechazó a los complejos, no eran números verdaderos, y dijo que eran imaginarios, término que se quedaría como consignación de estos números. Para Newton se trataba de raíces imposibles.

Sea como sea, el uso de métodos algebraicos expandió las fronteras de lo que debía considerarse números. El proceso, sin embargo, tomó mucho tiempo para esclarecerse plenamente. 

Bombelli

Otro resultado de la época fue el uso de las fracciones continuas. Por ejemplo, Bombelli las usó para aproximar raíces cuadradas (Algebra, 1 572), y, algunas décadas después, John Wallis para representar

Arithmetica Infinitorum, 1 655). Debe recordarse que los hindúes habían trabajado mucho las fracciones continuas para resolver ecuaciones indeterminadas.

Dos obras aritméticas tuvieron influencia durante los siglos XV y XVI: Triparty en la science des nombres de Nicolás Chuquet (francés) y la Summa de arithmetica, geometrica, proportioni et proportionalita de Luca Pacioli (1445 - 1514). 

Summa de arithmetica, geometrica, proportioni et proportionalita

En cuanto al primero, no se sabe cuánto es original de éste, y trata de las operaciones aritméticas racionales con números, incluye el estudio del sistema de numeración hindú-árabe. Hay, también, resolución de ecuaciones. Aunque este libro no fue publicado hasta 1 880, se sabe que Etienne de la Roche publicó en 1 520 y 1 538 un libro que contenía mucho del libro de Chuquet (Larismetique nouvellement composee).

El segundo libro era un compendio de aritmética, álgebra, geometría elemental y contabilidad (de doble entrada). Tampoco se puede decir que fuera original, no cita fuentes, por ejemplo. En su parte aritmética, explica métodos para multiplicar y hallar raíces cuadradas, en la de álgebra da las soluciones normales para ecuaciones lineales y cuadráticas. 

Mientras tanto, en el álgebra no se daría ningún desarrollo durante el Renacimiento hasta el trabajo de Cardano (Ars Magna, 1 545). No obstante, debe mencionarse el trabajo de Pacioli: Summa de Arithmetica, Geometria, Proportione et Proportionalita, 1 494, una recopilación de conocimientos y aplicaciones prácticas que, sin embargo, no tenían mucho más que lo que contenía el Liber Abaci de Leonardo de Pisa en 1 202. Podemos afirmar que:

"Parece haber consenso entre los historiadores de este periodo en que las matemáticas del Renacimiento se caracterizaron por el desarrollo del álgebra, no siguiendo el influjo geométrico griego, sino más bien las tradiciones medievales. Aunque las ciudades italianas sirvieron para la penetración de la ciencia árabe y griega antigua, también debe reconocerse la existencia de trabajos germánicos en el álgebra. Una de las más importantes de éstas fue la Aritmética íntegra de Stifel (un tratado del álgebra muy completo de lo que existía en la época publicado en 1 544).'' [Ruiz, A. y Barrantes, H.: Elementos de Cálculo Diferencial. Historia y ejercicios resueltos, p. 51]

Las ecuaciones de tercer y cuarto grados

Scipione dal Ferro

Las cuadráticas fueron resueltas desde los babilonios, usando el método de completar cuadrados.  Con relación a la de tercer grado, Pacioli pensó que no era resoluble, sin embargo alrededor del  1500 algunas de ellas fueron resueltas por Scipione dal Ferro (1 465 - 1 526) de Bologna:  

Un siguiente paso lo dio el famoso matemático Tartaglia, cuyo nombre era Niccolò Fontana de  Brescia (1499 - 1557). Su seudónimo se debía a que quedó tartamudo después de que un soldado  francés le cortara la cara. Resolvió varios tipos de ecuaciones de la forma:  

Cardano quien publicó en su Ars Magna el método de solución de Tartaglia se lo atribuyó con su discípulo Lodovico Ferrari (1 522 - 1 565) a dal Ferro, provocando una disputa con Tartaglia. Con la solución de la ecuación cúbica, luego, se obtuvo la solución de la cuadrática, por medio de Ferrari.

Entonces, por el concurso de Tartaglia, Cardano y Ferrari se encontraron métodos para la resolución de las ecuaciones de tercer y cuarto grados. Pero, tiempo después, Vieta, además de la generalización que logró con el simbolismo, exploró un método general para usar en cualquier tipo de ecuación sin importar el grado. 

Estos métodos desarrollados, de algunas maneras, se enseñan en la teoría elemental de las ecuaciones. Asuntos como la relación entre el grado y el número de raíces, o las calidades de éstas: cuántas positivas, negativas, complejas.

Cabe mencionar que Descartes, tiempo después, en La Géométrie, sugeriría la regla de los signos para las raíces: el número máximo de raíces positivas de P(x)=0 , con P(x) un polinomio, es el número de alteraciones en el signo de los coeficientes y el máximo de las negativas es el número de veces que dos signos + o - dos signos ocurren sucesivamente. Y, además, en ese mismo libro estableció el teorema del factor, es decir que: f(x) es divisible por x-a , con a positivo, si y solo si a es una raíz de f(x)=0. Y por x+a si a es un raíz ``falsa''.

Descartes realmente estableció el método moderno para encontrar raíces racionales de polinomios. Asuntos de la obra del genial francés que no son tan conocidos.

Otro resultado interesante de esta época es el uso del Triángulo de Pascal, que aunque lleva el nombre de este genial matemático fue usado anteriormente por otros como Tartaglia, Stifel y Stevin.

La expansión para con n entero, el llamado teorema del binomio, era conocida por los árabes del siglo XIII.
En la teoría de números de la época, el principal impulso lo llegó a realizar Pierre de Fermat (1601 - 1665), quien partiendo del trabajo de Diofanto estableció la dirección de los trabajos en esta disciplina matemática por lo menos hasta Gauss. Ya desarrollaremos esto con detalle.

El progreso en los símbolos

Se suele reconocer que fue el mejoramiento del simbolismo en el álgebra uno de los resultados relevantes del siglo XVI, aunque no se tuviera plena conciencia de su importancia. Por ejemplo, desde el siglo XV, se usó p por más y m por menos, y en el mismo siglo por los alemanes los símbolos de + y - . El símbolo 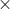para indicar "veces'' se le debe a Oughtred. Leibniz, años después, objetó que podía ser confundido con la x. Robert Recorde (1510 - 1558) introdujo el signo = . Para la igualdad Vieta usó ~ y Descartes ∝

Fue Thomas Harriot quien introdujo los signos < y >. Descartes usó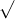

Vieta 

 

Probablemente fue Vieta quien realizó el salto más relevante en el simbolismo para el álgebra. Bajo  la influencia de Cardano, Tartaglia, Bombelli, Stevin y especialmente Diofanto, introdujo letras  para designar números de manera sistemática y consistente. Usó consonantes para las cantidades conocidas y vocales para las desconocidas. Su conciencia del papel del simbolismo y de la naturaleza general del álgebra lo llevó a hacer la famosa distinción entre logistica numerosa y  logistica speciosa para separar aritmética y álgebra. Mientras que la numerosa refería a números, la  speciosa a un método de operar sobre formas de cosas o especies, de ahí el nombre precisamente. Es decir, álgebra refiere a tipos generales. Una de las cosas que trató de hacer fue establecer las identidades algebraicas que había en los textos geométricos griegos de la Antigüedad.

Aunque muchos buscaron mejorar el trabajo de Vieta como Harriot, Girard y Oughtred, debe mencionarse que fue Descartes quien usó las primeras letras del alfabeto para cantidades conocidas y las últimas para las desconocidas, exactamente como se trabaja ahora (aunque Vieta y Descartes usaron los coeficientes literales solo para números positivos).

Leibniz, debe decirse, fue de los matemáticos más preocupados con el simbolismo. 

Logaritmos: un resultado relevante

Puede decirse que el resultado más relevante de la aritmética de los siglos XVI y XVII fueron los logaritmos. Aparentemente, fue Stifel el primero en notar la correspondencia entre los términos de la sucesión geométrica 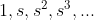y aquellos de la progresión aritmética formada por sus exponentes: 0, 1, 2, 3, 4,....

Al multiplicarse dos términos de la geométrica, el exponente del nuevo término así formado es la suma de los términos correspondientes en la aritmética. La división en la geométrica da la resta en la aritmética.

También Chuquet había notado esto (1484).

Pero fue John Napier (1550 - 1617) quien desarrolló los logaritmos, casi al terminar el siglo XVI, analizando la correspondencia entre las dos progresiones. Su motivación era, como era común en toda esta época, facilitar cálculos en trigonometría esférica que se usaba en asuntos de astronomía (de hecho, considera logaritmos de senos). Napier envió en consulta sus resultados al gran astrónomo Tycho Brahe. Dos obras condensan esos resultados: Mirifici Logarithmorum Canonis Descriptio y Mirifici Logarithmorum Canonis Constructio, de 1614 y 1619 respectivamente.

Otro matemático que trabajó con logaritmos fue Henry Briggs (1561 - 1631), quien sugirió el 10 como base, simplificando las cosas, y creó tablas de logaritmos para números cercanos que todavía tienen alguna utilidad.

Un tratamiento similar al de Napier fue realizado por el suizo Joost Bürgi (1552 - 1632) quien, para que se aprecie la conexión astronómica, fue asistente de Kepler en Praga.

Tiempo después se construyeron otras tablas de logaritmos por vía algebraica, incluso usando <series infinitas: James Gregory, Lord Brouncker, Nicholas Mercator, John Wallis y Edmond Halley ("padre'' del famoso cometa Halley).

Una nueva relación

Marino Ghetaldi

En este punto es relevante valorar la relación entre álgebra y geometría. Como herencia de los griegos, a pesar de los desarrollos en álgebra, siempre había una dependencia de la geometría. El punto de fondo refería a la justificación del álgebra, mejor dicho del pensamiento algebraico. Los matemáticos trataron primeramente de encontrar pruebas geométricas para asegurar el álgebra (como Cardano, Tartaglia, Pacioli o Ferrari). 

Una dosis mayor de independencia se logró con los trabajos de Vieta y los de Descartes. En un principio el álgebra buscó servir como un método para sistematizar situaciones de la geometría, en las construcciones. Es ésta la motivación principal que se encuentra en el trabajo de Vieta In Artem Analyticam Isagoge. Se identificaba una contraposición entre álgebra y geometría equivalente a la que existe entre análisis y síntesis.

Vieta afirmaba el álgebra como un "arte analítico''. El método analítico vislumbrado era asumir lo que se desea probar y por deducción llegar a verdades conocidas. Vieta buscó tratar los asuntos de proporciones de las magnitudes por medio del álgebra.

Esta relación mutua entre álgebra y geometría para estudiar las soluciones de problemas geométricos o, inversamente, para construir raíces de problemas geométricos, también se puede apreciar en obras del discípulo de Vieta, Marino Ghetaldi (1566 - 1627): Apollonius Redivivus y De resolutione et compositione matematica.