Cálculo Infinitesimal: Newton vs. Leibniz

El trabajo de Newton fue anterior al de Leibniz, pero que este último obtuvo sus resultados de una manera independiente a Newton

Si bien es cierto que Newton no había publicado antes de 1687 sus hallazgos en el cálculo diferencial e integral, obtenidos alrededor de los años 1665 y 1666, sí había presentado algunos de sus manuscritos a sus amigos. De Analysi, por ejemplo, se lo había dado a Barrow en 1669, quien se lo había enviado a John Collins. Leibniz estuvo París en 1672 y en Londres en 1673 y estuvo en contacto con gente que conocía la obra de Newton. Fue en este escenario que nació la acusación a Leibniz como un plagiador de las ideas de Newton.

Los historiadores de las matemáticas han concluido que el trabajo de Newton fue anterior al de Leibniz, pero que este último obtuvo sus resultados de una manera independiente a Newton. Se sabe, sin embargo, que ambos tuvieron la influencia de Barrow, quien se considera el matemático que había llegado más lejos en la comprensión de que la derivada y la integral tenían una naturaleza inversa, aunque con una óptica esencialmente geométrica.

Más aún, existe una diferencia radical en los enfoques de Newton y Leibniz en relación con el cálculo. Esto debería haber sido suficiente como para concluir que se trataba de creaciones independientes. Sin embargo, se desarrolló una gran polémica sobre la prioridad en estos descubrimientos o construcciones, que estableció una separación fuerte entre los matemáticos británicos y los continentales.

Para algunos, la responsabilidad en esta extraordinaria controversia, que tuvo implicaciones importantes en el desarrollo de las matemáticas, descansa fundamentalmente en Newton. Hawking es muy crítico de Newton:

"Aunque sabemos ahora que Newton descubrió el cálculo años antes que Leibniz, publicó su trabajo mucho después. Sobrevino un gran escándalo sobre quién había sido el primero, con científicos que defendían vigorosamente a cada uno de sus contendientes. Hay que señalar, no obstante, que la mayoría de los artículos que aparecieron en defensa de Newton estaban escritos originalmente por su propia mano, ¡y publicados bajo el nombre de amigos! Cuando el escándalo creció, Leibniz cometió el error de recurrir a la Royal Society para resolver la disputa. Newton, como presidente, nombró un comité 'imparcial' para que investigase, ¡casualmente compuesto en su totalidad por amigos suyos! Pero eso no fue todo: Newton escribió entonces él mismo los informes del comité e hizo que la Royal Society los publicara, acusando oficialmente a Leibniz de plagio. No satisfecho todavía, escribió además un análisis anónimo del informe en la propia revista de la Royal Society. Después de la muerte de Leibniz, se cuenta que Newton declaró que había sentido gran satisfacción 'rompiendo el corazón de Leibniz'''.

Producto de la polémica, los matemáticos británicos se negaron a usar la notación de Leibniz, que resultaba mejor que la de Newton y que es la que esencialmente usamos hoy en día. Se dio lo que se puede caracterizar como un retroceso de la matemática en Inglaterra en relación con la Europa continental. El asunto no se zanjaría sino hasta principios del siglo XIX cuando los británicos
adoptaron la notación de Leibniz. En la solución de la controversia, tuvo especial relevancia el papel jugado por el matemático francés Laplace.

Laplace

Esta polémica nos revela cómo en la construcción matemática participan dimensiones muy humanas, psicológicas, sociológicas, que influencian notablemente los quehaceres más abstractos dentro de las comunidades matemáticas. Es posible, incluso, que divergencias de criterios, decisiones, apreciaciones, o malas intenciones, puedan definir por años el decurso de una disciplina.

¿Cuáles eran las diferencias existentes en los enfoques de Newton y Leibniz?

Tanto Newton como Leibniz consideraron el cálculo como un nuevo campo matemático independiente tanto de la geometría como del álgebra, en sus conceptos y métodos, y ofrecieron un fundamento algebraico a éstos. Como lo hemos analizado, los métodos infinitesimales antes de Newton y Leibniz, tenían una gigantesca influencia de la geometría. El énfasis puesto ahora en el álgebra era decisivo. De igual manera, tanto Newton como Leibniz redujeron los problemas del cálculo de áreas, segmentos, volúmenes, a procesos de antiderivación. O, puesto de forma general, todos los grandes problemas que dieron origen a la construcción del cálculo fueron resueltos por ambos matemáticos en términos de derivación o integración (antiderivación).

Sin embargo, había diferencias. Mientras que Leibniz usaba los incrementos infinitesimales en la x y y, y luego estudiaba la relación entre ellos, Newton usaba sus infinitesimales en la derivada misma.
En Newton los infinitesimales estaban asociados directamente al cálculo de velocidades instantáneas (un claro sentido de aplicación física).
En Leibniz el interés no era la aplicación física. De hecho, se podría establecer una correlación entre infinitesimales y "mónadas'', estos últimos entes primarios en la descripción de lo real según la filosofía que aparece en su libro de filosofía (metafísica) Monadología.
El énfasis de Newton era la razón de cambio, mientras que en Leibniz lo era la suma infinita de infinitesimales.

Como hemos visto, fue también relevante la diferencia en el uso de la notación. Mientras que para Leibniz era muy importante, Newton no le prestó mucho cuidado. Tampoco Newton dio mucha atención a la formulación precisa de los algoritmos y reglas usuales del cálculo. En esto, nos repetimos, es probable que la vocación por una búsqueda de reglas generales universales, en Leibniz, fuera un factor para su desarrollo de la forma y la notación.

∫eibniz | Cálculo Infinitesimal

Leibniz nació en Leipzig y vivió casi siempre alrededor de Hanover, Alemania, donde trabajó para  los duques (uno de ellos fue Rey de Inglaterra con el nombre de Jorge I). Estudió derecho e hizo su  primera tesis en lógica.

Actual Leipzig

En 1666, escribió su tesis doctoral De Arte Combinatoria ("Sobre el arte de las combinaciones''), en la que formuló un método universal para razonar.

Se trataba de un hombre de grandes cualidades intelectuales que además de matemático, fue filósofo, abogado, filólogo, historiador e incluso hizo aportes a la geología. Aunque sus contribuciones no llegan al nivel de las de Newton, hizo contribuciones en mecánica, óptica, hidrostática, neumática, ciencia náutica, en la lógica y hasta en la construcción de máquinas calculadoras. Se ganó la vida como diplomático y abogado, pero sus trabajos en las matemáticas y la filosofía fueron muy relevantes. 

Calculadora de Leibniz

 

Se dice que siempre trató de conciliar las religiones católica y protestante. También fue un promotor de sociedades académicas con el propósito de promover las ciencias y las técnicas en reacción al carácter conservador y retrógrado de las universidades de su tiempo. Al igual que Galileo, escribió en lengua vernácula, privilegió el alemán frente al latín.

Leibniz propuso un método universal para conocer, crear y entender la profunda unidad del universo: la scientia generalis. Y también la creación de un lenguaje perfecto para realizar el razonamiento por medio de cómputos simples: la lingua characterica.

Estos proyectos motivaron parte de su trabajo intelectual, y le condujeron en el primer caso a resultados matemáticos, y en el segundo a ofrecer aportes en la lógica y en la simbología matemáticas. 

Es interesante que Leibniz fue influenciado por Descartes de una manera particular. Este último tuvo una influencia importante en los matemáticos holandeses; debe recordarse que pasó unos veinte años en Holanda. Tuvo influencia en particular sobre Frans van Schooten (1615 – 1660) quien propagó y amplió la geometría analítica cartesiana, e incluso hizo una versión en latín de la Géométrie. Huygens fue uno de los discípulos de van Schooten, un gran científico con aportes en la teoría de la luz, en astronomía y al que se le atribuye el reloj de péndulo. En 1666, Huygens se trasladó a París, en donde permaneció hasta 1681. Este matemático, ya en 1656, había aplicado métodos infinitesimales a las cónicas (por ejemplo, redujo la "rectificación'' de la parábola a la "cuadratura'' de la hipérbola). 

Frans van Schooten

Leibniz estuvo en París, al parecer, entre los años 1673 y 1676. Por influencia directa de Huygens estudió los trabajos de Descartes, Pascal y algunos matemáticos británicos. La relación entre Leibniz y Huygens fue importante para el trabajo de Leibniz en el cálculo. Es posible ver la relación entre estos dos matemáticos en el desarrollo conjunto del concepto de energía cinética. 

Se debe mencionar que Leibniz sabía del rumor de que Newton ya manejaba un nuevo método, y esto contribuyó a estimular su trabajo.

Mientras el enfoque de Newton fue físico, el de Leibniz fue esencialmentegeométrico, incluso algebraico o lógico.

Desde que Leibniz entró en contacto con las matemáticas, bajo la influencia de Huygens, le dio importancia al cálculo de las tangentes a las curvas y, muy rápidamente, estuvo seguro de que se trataba de un método inverso al de encontrar las áreas y volúmenes a través de sumas. Leibniz escribió varios artículos entre 1675 y 1684 que expresan su evolución en la construcción del cálculo. En noviembre de 1676 ofreció las reglas dxⁿ= ndx^n-1  para un entero o fraccional y, también

En julio de 1677 Leibniz ofrecía las reglas correctas para la diferencial de la suma, diferencia, producto y cociente de 2 funciones y para potencias y raíces, aunque no ofrecía pruebas.

Su método se recoge por primera vez en un artículo que apareció en la revista Acta eruditorum en 1684, que él mismo había fundado dos años antes (donde ya había anunciado su método): Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationales quantitates moratur, et singulare pro illis calculi genus ("Un nuevo método para máximos y mínimos, y también para tangentes, que no se ve obstruido por las cantidades fraccionarias ni por las irracionales''). 

Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationales quantitates moratur, et singulare pro illis calculi genus

Se trataba de una aproximación geométrica y no cinemática como en Newton. Se percibe la influencia de Pascal y de Barrow (especialmente Geometrical Lectures, 1670), así como de Huygens y Descartes. Ya aquí aparecían las reglas básicas de la derivación, las condiciones para valores extremos (máximos y mínimos) y para los puntos de inflexión.

Este artículo contenía, entonces, los símbolos dx, dy y las reglas

dy=0 para valores extremos relativos o  d²y=0 para los puntos de inflexión.

Fue Leibniz quien introdujo precisamente aquí el término "cálculo diferencial'' (de di-fe-ren-cias).
Aunque y se toman como funciones de , el término "función'' no aparece en este artículo. Este término aparecerá hasta 1692 en otro artículo.
Antes de usar "cálculo diferencial'' había usado la expresión "methodus tangentium directa''. También "methodus tangentium inversa'' o "calculus summatorius'' para la integración definida y, en 1698, "calculus integralis'' (específicamente, en un artículo con Jean Bernoulli).
Fue en el año 1686 cuando Leibniz hizo una publicación sobre la integración donde recogía el símbolo "∫''. No obstante, ya había utilizado otros símbolos para la noción de integral: primero omn. y (todas las y), luego ∫y  y luego ∫ydx.

En 1675, usó la siguiente notación: 

omn. => quería decir suma (del latín omnia),
 
l => significa dy

Por ejemplo, omn.l = y queria decir en nuestra notación ∫dy=y y  

Para Leibniz: dy y dx representaban cantidades arbitrariamente pequeñas (diferenciales o infinitesimales), y con ellas iría construyendo tanto su cálculo integral (sumas) como su cálculo diferencial (cálculo de tangentes). Los símbolos de Newton se traduce como dx y dy en Leibniz.

Los trabajos de Leibniz tuvieron una gran repercusión y potenciaron un desarrollo muy rápido del cálculo con su enfoque. En muy poco tiempo, por ejemplo, y con la contribución relevante de los hermanos Bernoulli, se puede decir que se tenían los resultados básicos de lo que hoy se enseña en los cursos de cálculo universitario.

Posteriormente, Euler y otros matemáticos de la Europa continental darían continuidad a esta obra. Debe decirse que el enfoque de Newton, por medio de su teoría de fluxiones, tuvo un desarrollo más limitado con Taylor, Maclaurin y otros matemáticos británicos. Ya volveremos sobre esto.

Los símbolos “=” y “x” serían aceptados de manera dominante debido a su influencia. Los términos de función y coordenadas también son resultado de la labor de Leibniz.

Leibniz al igual que Newton también fue atacado por otros intelectuales de la época. El médico y geómetra Bernard Nieuwentijdt (1654 - 1718) en 1694 señalaba que había oscuridad en el trabajo de Leibniz y que no podía entender cómo diferían las "cantidades infinitamente pequeñas'' de 0, y preguntaba cómo una suma de infinitesimales podía dar algo finito. 

Bernard Nieuwentijdt

Debe decirse que ni Leibniz ni Newton pudieron ofrecer una gran precisión y mucha claridad lógica en los fundamentos de sus métodos en el cálculo diferencial e integral. Para ellos lo decisivo era la coherencia en sus resultados y la fecundidad de los nuevos procedimientos. Eso era suficiente para generar el progreso de esta nueva disciplina matemática.

La motivación fundamental de Leibniz por un método universal para obtener conocimiento, invenciones y mostrar o entender la unidad del mundo, la búsqueda por una ciencia general, una caracteristica generalis, lo colocó en la trayectoria del descubrimiento del cálculo.

La influencia de Leibniz sobre sus contemporáneos es directa. Por ejemplo, los hermanos Bernoulli realizaron un gran desarrollo de estos métodos. Un texto de cálculo apareció en el año 1696, titulado Analyse des infiniment petits, escrito por el marqués de L'Hôpital, que incluyó muchos resultados de Johann Bernoulli.

Algo relevante en Leibniz son sus contribuciones a la notación matemática. Influido por esa otra gran pretensión, aparte de una ciencia general, la creación de una lengua universal que impidiera los errores de pensamiento y redujera éste al cómputo, la lingua universalis, este brillante pensador dejó una herencia extraordinaria en la simbología de las matemáticas. Incluso, lo que ya mencionamos, el nombre de cálculo diferencial y cálculo integral encuentran su origen en él. Aunque se le atribuye su nombre a Leibniz las siguientes series fueron desarrolladas por James Gregory, quien contribuyó mucho al manejo de los procesos que lidiaban con el infinito: 

Isaac Newton | Cálculo Infinitesimal | Teoría de fluxiones

Es interesante mencionar que las principales ideas que Newton desarrollaría fueron concebidas en un período muy corto de tiempo, mientras permanecía en su lugar de nacimiento para escapar de la peste en Cambridge. Entre 1665 y 1666 concibió: las leyes de la gravitación universal y la mecánica celeste, las leyes de la composición de la luz, el teorema del binomio, y el cálculo.

El siglo XVII fue decisivo para las ciencias. Una combinación de resultados ofreció una nueva pintura de la realidad y nuevas perspectivas para el conocimiento. Por ejemplo, se dieron varios desarrollos importantes en la óptica y en el estudio de la naturaleza de la luz con Grimaldi (1618-1663) y el mismo Newton. Huygens hizo una descripción matemática del funcionamiento ondulatorio de la luz. Torricelli (1608 - 1647), discípulo de Galileo, inventó el barómetro descubriendo la presión atmosférica y también el "vacío''. Gassendi (1592 - 1655) introdujo de nuevo una forma de la teoría atomista de Leucipo y Demócrito. Es la época de Boyle, con sus resultados sobre el vacío y la teoría de gases, y también de Hooke, a quien se le atribuye haber sido el principal físico experimental antes de Faraday. Ahora bien, fue la obra de Newton la que culmina y potencia la llamada Revolución Científica.

La teoría newtoniana de la gravitación universal terminó de destruir la cosmología anterior y con ello se abrirían nuevas perspectivas intelectuales.

Un dato curioso es que Isaac Newton nació en 1642, en el campo, en Woolsthorpe, Inglaterra precisamente el año de la muerte de Galileo. Huérfano de padre antes de nacer, estudió en la Universidad de Cambridge gracias al apoyo de un tío materno (que se había graduado en esa universidad) que se dio cuenta de los talentos del niño. Newton haría aportes decisivos en las matemáticas, la mecánica, la cosmología, el estudio de la luz, que establecieron, en realidad, una nueva visión del universo y potenciaron significativamente nuevos métodos para el progreso de las ciencias. 

Manzano en la Universidad de Cambridge

Newton estudió en Cambridge con Barrow y permanecería en ese lugar hasta 1696.

Newton realizó una gigantesca hazaña intelectual: la mecánica celeste, es decir aquella síntesis magistral de mecánica y astronomía que integraba las leyes de Kepler (establecidas empíricamente), el movimiento de las mareas, el problema de los dos cuerpos esféricos, los principios de la teoría del movimiento lunar y muchas otras cosas, integración del movimiento de los astros y las leyes de la mecánica terrestre, de los resultados de Copérnico y Kepler con los de Galileo, y ofrecía al mundo una descripción matemática de la realidad.

Philosophiae naturalis principia mathematica

 

Una de las obras más famosas e influyentes de todos los tiempos: Philosophiae naturalis principia mathematica ("Principios matemáticos de la filosofía natural'') es de 1687. Esta obra integra matemáticamente las leyes del movimiento planetario a través de la ley de la gravitación de los cuadrados inversos: 

[La fuerza gravitacional entre dos masas es proporcional a las masas e inversamente proporcional al cuadrado de la distancia entre ellas] o

[La fuerza gravitacional entre dos masas es igual a una constante por el producto de las masas, dividido este por el cuadrado de la distancia entre ellas. G es la constante de proporcionalidad.]
Conviene una descripción de este libro fundamental:

"En resumen, los Principios Matemáticos de la Filosofía Natural se presentan como un tratado de mecánica en el que se establecen demostrativamente los movimientos de los cuerpos en sus relaciones generales con las fuerzas que los producen. La obra está dividida en tres partes o libros. El Libro I se ocupa del movimiento de los cuerpos en el vacío, esto es, en un medio carente de toda resistencia. En él jugará un importante papel la noción de fuerza centrípeta, a partir de la cual se fundamentan dinámicamente las tres leyes de Kepler. El Libro II, en cambio, estudia el movimiento de los cuerpos en medios resistentes (fluidos). Constituye de hecho una implacable crítica a la teoría cartesiana de los vórtices. Por último, el Libro III ofrece la constitución del sistema del mundo como consecuencia de la aplicación de la matemática racional (en la que movimientos y fuerzas se analizan matemáticamente y en abstracto) a la mecánica celeste. Es decir, los resultados de los libros anteriores, en especial del Libro I, se emplearán para conocer y predecir con exactitud los principales fenómenos celestes y terrestres, quedando finalmente instituida la famosa teoría de la gravitación universal. Cuando esto suceda, el mundo aparecerá como una elegante estructura ordenada en la que nada, ni en los cielos ni en el mar, escapará a la acción de esa fuerza gravitatoria que opera por doquier según una ley inexorable desvelada por Newton.'' [Rioja, Ana & Ordóñez, Javier: Teorías del Universo, Volumen II de Galileo a Newton, pp. 198, 199]

En opinión de Hawking esta obra es:

"Probablemente la obra más importante publicada en las ciencias físicas en todos los tiempos. En ella, Newton no solo presentó una teoría de cómo se mueven los cuerpos en el espacio y en el tiempo, sino que también desarrolló las complicadas matemáticas necesarias para analizar esos movimientos. Además, Newton postuló una Ley de la Gravitación Universal, de acuerdo con la cual cada cuerpo en el Universo era atraído por cualquier otro cuerpo con una fuerza que era tanto mayor cuanto más masivos fueran los cuerpos y cuanto más cerca estuvieran el uno del otro.''

Newton explicó matemática y axiomáticamente el movimiento de los cuerpos celestes, las mareas, los fundamentos de la teoría del movimiento lunar, etc.

En la perspectiva cosmológica:

"La teoría de Newton pondrá de manifiesto la posibilidad de un conocimiento racional del universo copernicano a partir de principios mecánicos, en el que ya no tenga el menos sentido la distinción entre mundo sublunar y otro supralunar o entre Tierra y Cielo, en el que el conjunto de los cuerpos ocupen un lugar no especifico de cada uno de ellos en un espacio y tiempo infinitos, en el que nada escape a la acción de la gravedad, en el que todo en cualquier parte del sistema solar esté sometido a los mismos procesos de movimiento regidos por las mismas leyes naturales inexorables.

Si el De Caelo de Aristóteles fue la obra cosmológica indiscutible durante siglos ligada a una astronomía geocéntrica, los Principia de Newton representan la culminación de una concepción realista heliocéntrica de la astronomía debido al carácter dinámico, y no meramente cinemático, de su teoría. En efecto, tal como manifiesta el astrónomo Fred Hoyle, si la opinión según la cual es la Tierra la que realmente gira alrededor del Sol tiene validez objetiva, ha de haber alguna propiedad física importante que aparezca en el planteamiento heliocéntrico, pero no en el geocéntrico. ¿Cuál? En el sistema solar la ley de gravitación o ley del inverso del cuadrado arroja resultados incompatibles aplicada a un mundo en el que el centro sea el Sol y a otro en el que lo sea la Tierra, puesto que predice órbitas planetarias diferentes según el centro elegido. Ahora bien, las predicciones que concuerdan con la observación son las que corresponden a un centro ocupado por el Sol, y no en modo alguno por la Tierra. Luego la ley de Newton sólo opera en un mundo heliocéntrico, lo que pone de manifiesto la verdad, y no simplemente la utilidad del sistema copernicano.'' [Rioja, Ana y Ordóñez, Javier: Teorías del universo. Volumen I. De los pitagóricos a Galileo, p. 273]

Principia es uno de las grandes libros de todos los tiempos. No obstante, en el año 1704 Newton publicó otro gran trabajo, la Óptica, donde formula su teoría corpuscular de la luz y su teoría de los colores. En ediciones posteriores Newton incluyó como apéndice algunos tópicos sobre filosofía natural, con consideraciones especulativas y metafísicas sobre asuntos como la luz, el calor, el éter, la materia.

Newton dio a su cálculo el nombre de Teoría de fluxiones

Es interesante mencionar que las principales ideas que Newton desarrollaría fueron concebidas en un período muy corto de tiempo, mientras permanecía en su lugar de nacimiento para escapar de la peste en Cambridge. Entre 1665 y 1666 concibió: las leyes de la gravitación universal y la mecánica celeste, las leyes de la composición de la luz, el teorema del binomio, y el cálculo.
Sin lugar a dudas, el cálculo diferencial e integral dentro de las matemáticas

Leibniz

constituía el resultado más importante del siglo XVII y abría nuevos territorios y fronteras extraordinariamente fértiles para potenciar el desarrollo de estas disciplinas, y de la ciencia en general. La obra de Newton y, como veremos, la de Leibniz también, empujaron una nueva época en la construcción matemática.
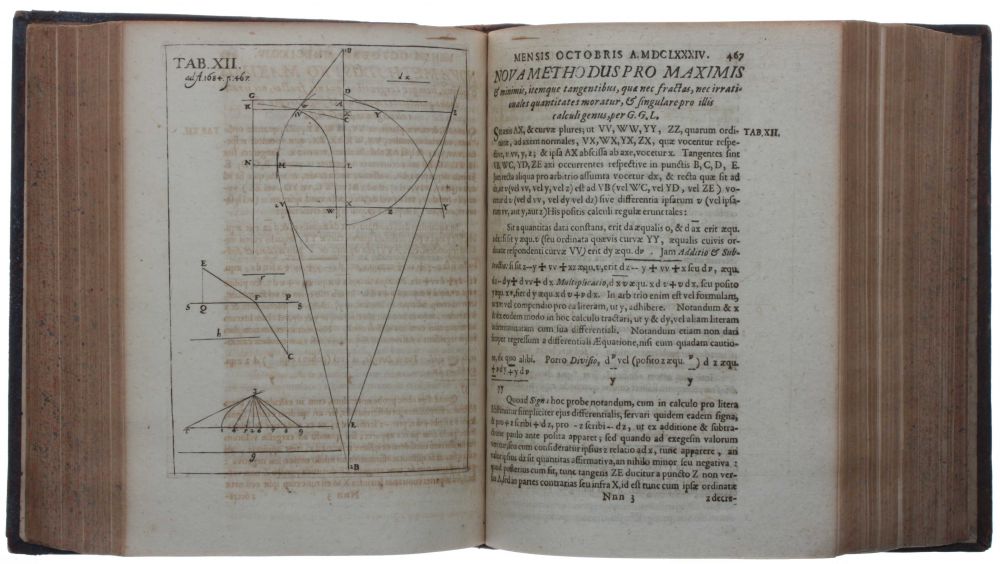
Aunque Newton descubrió-construyó el cálculo diferencial e integral en los años 1665 a 1666, y Leibniz lo hizo en 1673 y 1676, fue este último quien publicó primeramente sus resultados en los años 1684 y 1686. Newton publicaría sus resultados en 1704 y 1736. Sin duda, Newton y Leibniz aportaron sus conceptos y métodos de una manera totalmente independiente, más aún con características y fisonomías diferentes, pero -lo que es la vida- se estableció una polémica durante muchos años sobre quién había hecho sus descubrimientos primero.
Newton dio a su cálculo el nombre de Teoría de fluxiones. Las funciones x, y, z eran fluentes, y las derivadas las llamaba fluxiones, estas últimas las denotaba.

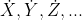
Los infinitesimales los llamaba Momentos de fluxiones y los denotaba

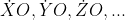
Los métodos infinitesimales eran el nudo teórico al que buscaban dar una respuesta tanto Newton como Leibniz. De hecho, se trata de la noción de límite. Estos matemáticos obtuvieron sus resultados, métodos, aplicaciones, usando esa noción de una manera intuitiva, física, geométrica, mecánica. Como veremos, un tratamiento más riguroso se desarrollaría muchas décadas después.

Los métodos infinitesimales habían estado en la historia de las matemáticas

La paradoja de Aquiles y la tortuga. Indicios de
cálculo infinitesimal

desde la Antigüedad, ya sea cuando se abordaron los problemas del infinito y la continuidad, incluso por medio de las paradojas de Zenón, como también en la series o sumas indefinidas de términos, en la división indefinida de longitudes, áreas o volúmenes, etc. Son métodos infinitesimales a los que se hace referencia con los procedimientos arquimedianos de exhausción para calcular longitudes áreas o volúmenes. Es, también, este tipo de método el que se plantea cuando se divide un área en un número infinito de rectas indivisibles, o se calcula un área usando una cantidad infinita de rectángulos, etc..

Críticas 

 

Es interesante traer a colación aquí, que, precisamente, por la falta de precisión y rigor lógicos en el trabajo de Newton en relación con el cálculo, se desató una serie de críticas por parte de filósofos.

Uno de los más conocidos fue el obispo George Berkeley (1685 - 1753). Berkeley reconocía la utilidad de los nuevos métodos y la validez de los resultados, pero criticaba que no se apegaban a la deducción lógica y más bien eran procedimientos inductivos. Newton afirmaba que la derivada era una razón final y consideraba los infinitesimales como "cantidades evanecentes''.

Para Berkeley la noción de velocidad instantánea no podía existir puesto que el concepto de velocidad depende del espacio y el tiempo. Si se expresa la velocidad como el límite

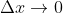
(Cuando ) de razones como

Con la y distancia x tiempo, Berkeley preguntaría ¿cuál es el sentido de incrementos que se desvanecen ( Δy y Δx se hacen 0) dejando un cociente sin sentido ? Una velocidad --para Berkeley-- debe ser una distancia sobre un tiempo. ¿Cómo puede existir una velocidad con  distancia nula y sobre un tiempo también nulo?

Lo que estaba en la picota era el "paso al límite'', porque se hacía sin suficiente precisión de los términos usados. Además, lo que es decisivo, ese paso de las pendientes de rectas secantes a la pendiente de la recta tangente o la derivada, es decir el límite, era un método que se escapaba de las matemáticas "normales''. La noción de "paso al límite'' no podía encerrarse dentro de la geometría euclidiana, la aritmética o el álgebra tradicionales. De lo que se trataba era de un método matemático diferente, nuevo, el cual se encontraba en esa época en un momento de descubrimiento-construcción en el cual no se podía pretender un nivel mayor de precisión. Antes tendría que desarrollarse un largo proceso de manipulación, aplicación, reflexión y afinamiento para poder acceder a una formulación más rigurosa desde un punto de vista lógico. 

La creación del cálculo diferencial e integral por Newton estuvo relacionada con las series infinitas

Por otra parte, la creación del cálculo diferencial e integral por Newton estuvo relacionada con las series infinitas. El descubrimiento y la generalización del teorema del binomio le permitieron hacer importantes desarrollos mediante series infinitas (aunque no siempre con la validez asegurada). Había una gran relación entre el trabajo de Newton y el estudio sobre la series infinitas que había hecho Wallis. 

analysi per aequationes numero terminorum

Newton escribió en el año 1669 sus ideas sobre series y el cálculo en el libro De analysi per aequationes numero terminorum infinitas que, sin embargo, fue publicado hasta 1711. También, esta relación entre series y cálculo se manifiesta en Methodus fluxionum et serierum infinitorum (escrito en 1671), y publicado en inglés en 1736 y en latín en 1742. Una tercera exposición del cálculo Newton la hizo en 1676 en De quadratura curvarum. En esta última obra, publicada en 1704, Newton trataba de evitar las "cantidades infinitamente pequeñas'' y las "cantidades fluentes'' que usó en los trabajos anteriores. Aquí planteaba una teoría de las "razones primeras y últimas'', donde la "razón última'' era la derivada formulada sin el concepto de límite.   

El único libro en que Newton mostró su cálculo y publicó rápidamente fue Philosophiae naturalis principia mathematica (1687). En el Lema I del Libro I, Sección I de esta obra, al considerar el límite de una función (o de la derivada), Newton señalaba:

"Cantidades, y la razón de cantidades, que en cualquier intervalo finito de tiempo convergen continuamente a la igualdad, y que antes del final de dicho tiempo se aproximan una a la otra más que cualquier diferencia dada, se hacen finalmente iguales''

Si bien Newton usó el cálculo en su estudio de la astronomía y mecánica en esta obra, una gran parte del libro fue expresada en forma geométrica tradicional para que sus contenidos fueran mejor aceptados por la comunidad científica de ese tiempo.

Stephen Hawking nos brinda una pincelada de la personalidad de Newton:

"Isaac Newton no era un hombre afable. Sus relaciones con otros académicos fueron escandalosas, pasando la mayor parte de sus últimos tiempos enredado en acaloradas disputas. Después de la publicación de los Principia Mathematica (seguramente el libro más influyente jamás escrito en el campo de la física), Newton fue ascendido rápidamente en importancia pública. Fue nombrado presidente de la Royal Society, y se convirtió en el primer científico de todos los tiempos que fue armado caballero.'' 

Las grandes cualidades de las personas suelen estar acompañadas de debilidades; la naturaleza de la vida es así. Los científicos son de carne y hueso y los resultados de su trabajo están condicionados por sus características personales y por el contexto social e histórico en que se dan. 

 

Uno de los problemas de Newton era esta distancia entre su creación intelectual y la publicación

Si bien Newton había descubierto o construido el cálculo alrededor del año 1665 no publicaría sus resultados hasta el siglo XVIII, en un período que va de 1704 a 1736. Leibniz lo había descubierto un poco después que Newton entre los años 1673 y 1676, pero lo publicó antes que él: entre 1684 y 1686.

De hecho, a la hora de establecer su influencia sobre sus contemporáneos, debe señalarse, uno de los problemas de Newton era esta distancia entre su creación intelectual y la publicación (entre 1665 y 1666 estaba en poder de la ley de la gravitación universal, la cual no aparecería sino hasta 1687).

Cálculo Infinitesimal | Primeros Pasos | Parte 2

El gran matemático Laplace consideraba a Fermat como el verdadero descubridor del cálculo diferencial

Fue en el curso de sus trabajos en la geometría de coordenadas que Fermat descubrió un método que le permitía calcular la pendiente de una recta tangente a una curva algebraica. Un claro antecedente del concepto de derivada. La forma precisa en que Fermat lo realizó se puede reducir al cálculo del siguiente límite: 

Esta aproximación es casi idéntica a la que Newton y Leibniz desarrollarían posteriormente. Es debido a este resultado que el gran matemático Laplace consideraba a Fermat como el verdadero descubridor del cálculo diferencial. Debe decirse, sin embargo, que Fermat no explicó apropiadamente su método. 

Barrow 

Por otra parte, otros matemáticos hicieron contribuciones previas al desarrollo definitivo del cálculo, como el mismo maestro de Newton, Isaac Barrow (1630 - 1677) en Lectiones Geometricae (1669). Para algunos historiadores de las matemáticas, había sido precisamente Barrow quien más cerca estuvo del cálculo diferencial e integral antes de Newton. Por ejemplo, se supone que Barrow era consciente de que los problemas de la tangente y del cálculo de áreas eran inversos. 

Barrow tuvo una participación importante en el trabajo de Newton. En 1669, cuando fue llamado a ocupar el puesto de capellán del rey Carlos II, Barrow logró que a Newton le dieran la Cátedra Lucasiana en Cambridge.

Es decir, a mediados de el siglo XVII, los matemáticos habían logrado calcular rectas tangentes, calcular volúmenes y centroides, aunque todavía la relación inversa entre la derivada y la integral no se había explicado; y esto último fue más bien un resultado del trabajo de Isaac Barrow, por lo menos desde 1670. Por otra parte, Pascal introdujo un método que adelantaba el "desvanecimiento'' de los famosos infinitesimales, es decir, el paso al límite. Deben consignarse también los trabajos de Grégoire de Saint Vincent, Paul Guldin y André Tacquet.

El nombre de Blaise Pascal se asocia con los infinitesimales, el principio de inducción completa, con las probabilidades, y a un famoso teorema de un hexágono inscrito en un círculo, así como al triángulo aritmético formado por coeficientes binomiales.

Áreas y curvas

Otro de los grandes asuntos a los que respondió el cálculo fue el de calcular áreas bajo curvas, ya con geometría de coordenadas, y un tema que es similar al de aproximar figuras por medio de otras; en la Antigüedad se usó el método de exhausción en esa dirección. Vamos a usar básicamente el tratamiento que dimos en nuestro libro Elementos de Cálculo Diferencial. Historia y Ejercicios resueltos para indicar un ejemplo de la situación.

Usamos la curva

entre la recta O y A

Dividimos el segmento en n partes; esto provoca de n segmentos de longitud , en el caso de n=4, las alturas son:


¿Cómo se aproxima el área? Por medio de la suma de los rectángulos de base siempre l. Es decir, tenemos:

Por lo tanto:

¿Por qué?
En el caso de n rectángulos, de base , las alturas son de la forma



y la última


¿Cómo queda el área? Así:


El problema es el segundo factor de la derecha. Pero, se podía resolver porque Pascal y Fermat habían demostrado que

¿Qué pasa cuando n se hace muy grande? Es decir, cuando n es infinito. Pues se eliminan. Tenemos de esa manera que:

Había otros resultados. Por ejemplo, Fermat había calculado (en nuestra notación)

Se trataba de un resultado conocido por Roberval, Torricelli y Cavalieri, más o menos.

La función: un concepto clave

Uno de los conceptos matemáticos que tienen origen directo en los trabajos de los científicos de la época es el de función. Tanto por su interés en el mejoramiento de los métodos y al calcular la posición de los barcos navegantes a través de la luna y las estrellas, como el movimiento de objetos en caída libre o de los proyectiles, se empezó a construir el concepto de función. Éste ya se encuentra, por ejemplo, en los trabajos de Galileo. No obstante, durante todo el siglo XVII, las funciones fueron estudiadas más bien como curvas. Incluso las funciones trascendentes elementales como las logarítmicas, exponenciales o trigonométricas.

También debe mencionarse la introducción de curvas viejas y nuevas por medio de movimientos. Por ejemplo, la cicloide fue definida por Mersenne en el año

Mersenne

1615. En la Antigüedad la cuadratriz y  la espiral de Arquímedes fueron definidas a través de movimiento.
Las curvas fueron agrupadas entre aquellas algebraicas y las trascendentes. Por ejemplo, James Gregory expresó con claridad en el año 1667 que el área del sector circular no podía ser una función algebraica del radio y de la cuerda. De igual manera, Leibniz demostró que la función sen x no podía ser algebraica en relación con x. Puede decirse, sin embargo, que la distinción se originó en Descartes, al separar curvas geométricas de las que él llamó mecánicas.

Los historiadores de las matemáticas afirman que el concepto de función en el siglo XVII, como una cantidad obtenida de otras a través de una colección de operaciones algebraicas u otras
operaciones, se encontraba plenamente en el trabajo de Gregory: Vera Circuli et Hiperbolae Quadratura (1667). Como veremos, Newton usaría la palabra "fluente'' para la relación entre las variables. Leibniz usaría la palabra función para una cantidad variable de punto en punto sobre una curva, como la longitud de la tangente, la normal, la ordenada. En 1714, Leibniz utilizaría la palabra función para cantidades que dependían de una variable.

Vera Circuli et Hiperbolae Quadratura (1667)

Wallis y Huygens

 

Otra de las obras significativas en la gestión del cálculo fue Aritmetica infinitorum, de Wallis, en 1655. Wallis utilizó procesos infinitos, como productos y series, potenciando el uso del álgebra y alejándose de los métodos geométricos de la Antigüedad.

Fue también de importancia la obra de Huygens Horologium oscillatorium de 1673, la cual aunque dirigida a técnicas en el cálculo del tiempo para la navegación, incluyó el estudio de curvas en el plano. Huygens trabajó con la catenaria, la tractriz, y la logarítmica. Tanto los trabajos de Wallis como los de Huygens fueron importantes para la síntesis teórica que haría Newton.

Christiaan Huygens