Matemáticas Hindú | Jainista | Bakhshali | Periodo Clásico

Jainista

Durante el periodo que va del 800 a.C. al 200 a.C. aparece lo que se llama las matemáticas jainistas.
El periodo jainista refiere a la declinación védica y al ascenso del budismo y el jainismo. Sabemos que existió en esta época una fascinación por los números grandes y que ofrecieron un primer concepto de infinito. Aquí aparecen operaciones como: 

(en el Anuyoga Dwara Sutra, siglo II o I a.C.)

Un tema importante que desarrollaron fue el de las combinaciones y permutaciones (por ejemplo en el Bhagabati Sutra, 300 a.C.). Hay fórmulas equivalentes a:

Se dio un importante tratamiento de las progresiones geométricas.

Bakhshali 

El periodo del 200 a.C. al 400 d.C. posee como referencia principal en lo que se refiere a las matemáticas, un manuscrito que fue encontrado en 1881 en un pueblo llamado Bakhshali, noreste de la India. Para la mayoría de expertos se trata de un documento del siglo XII d.C. pero una reescritura de textos del periodo que estamos considerando. Se trataba de un manual con reglas y ejemplos, esencialmente de álgebra y aritmética. 

manuscrito Bakhshali de su sistema númerico

Con base en ese manuscrito se puede decir que los problemas tratados tuvieron una asociación menos religiosa que la que tuvieron en los periodos védico o jainista, es decir: fueron más prácticos. Se elaboraron mejores aproximaciones de √2. Se amplió el trabajo de series realizado por los jainistas. Tenemos un sistema posicional con valor numérico, e incluido el cero. Se inició un interés por el análisis indeterminado y hay, en la exposición, cierta demostración de las reglas que se formulan y de las que se brindan ejemplos.

Vamos ahora al periodo clásico, que es el que más nos interesa en este capítulo.

El periodo clásico

Empezamos citando algunos astrónomos y matemáticos: Aryabhata I (nació alrededor del 476 d.C.), Brahmagupta (alrededor del 598), Mahavira (ca. 850), Sridhara (ca. 900), Bhaskara (nació 1 114), Narayana Pandit (ca. 1 370), Madhava de Sangamagramma (ca. 1 340 - 1 425) y Nilakantha Somayaji (1 445 - 1 545).

Aryabhata I

Aryabhata I, en un libro que se titula Aryabhatiya, da una descripción del conocimiento científico de la época, incluye un sitema de notación numérico alfabético, reglas de operaciones en aritmética y trata procedimientros para resolver ecuaciones simples y cuadráticas, y, también, ecuaciones indeterminadas de grado uno. Hay, además, trigonometría, la que incluye las funciones seno, una función que se llamaba seno verso que es igual al 1-coseno. Dio el valor de 3,1416 para π..Su obra fue continuada por Varahanihira (ca. 505 - 587) y por Bhaskara (ca. 600). Este último ofreció una solución de ecuaciones indeterminadas de primer grado, que ejerció una importante influencia sobre Brahmagupta.

Libro Aryabhatiya

Brahmagupta, en una obra llamada Brahma Sputa Siddhanta, ofreció un método para la resolución de ecuaciones indeterminadas de primero y segundo grados. En otra obra, Khanda Khadyaka, en trigonometría dio un procedimiento para calcular los senos de ángulos intermedios con base en una tabla dada de senos. Se dice que era equivalente a la fórmula de Newton-Stirling hasta las diferencias de segundo orden. El primer libro fue traducido por los árabes y luego por los europeo, con lo que así se ofreció a Europa el conocimiento de la astronomía y matemáticas hindúes.

Brahmagupta

Mahavira, matemático y no astrónomo, sintetizó y amplió los resultados de Aryabhata, Bhaskara y Brahmagupta. Se afirma que su obra Ganita Sara Samgraha es una culminación de los trabajos y tradiciones de los jainistas. Por ejemplo, en las permutaciones y combinaciones. Dio soluciones a varios tipos de ecuaciones de segundo grado. Amplió el tema de la ecuaciones indeterminadas. Y trabajó en geometría con triángulos rectángulos de lados racionales.

Sridhara, en Pataganita, ofreció un método para sumar series aritméticas y geométricas que sería relevante posteriormente.

Se considera una culminación de 500 años de trabajos matemáticos la obra de Bhaskara II (llamado también Bhaskaracharya: "maestro Bhaskara''), Lilavati. Un ejemplo, un método para resolver ecuaciones indeterminadas de la forma 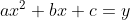(método "cíclico''). Este método fue redescubierto por William Brouncker en 1 657. Se afirma que en su obra hay rastros de análisis y cálculo infinitesimal.

Madhava de Sangamagramma

Se considera que Madhava de Sangamagramma fue probablemente el más importante de los astrónomos medievales de la India. En las matemáticas se dice que introdujo el salto del límite al infinito. 

Los hindúes tuvieron como característica relevante de su álgebra el uso de símbolos (por ejemplo, el punto para el cero o para incógnitas, en algún momento de la historia hindú) y las letras del alfabeto para denotar las incógnitas.

Las ecuaciones lineales de primer grado aparecieron en los Sulbasutras (el de Baudhayana), pero una solución algebraica aparece hasta el documento Bakhshali. Las de segundo grado como, por ejemplo, o , están en los Sulbasutras pero aparecen resueltos en el de Bakhshali también. Aquí se ofreció la respuesta 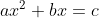ó , están en los Sulbasutras pero aparecen resueltos en el de Bakhshali también. Aquí se ofreció la respuesta

Sridhara y luego Mahavira ofrecieron la solución:

En relación con el primero, sin embargo, no se sabe si usó las dos raíces. Sobre las ecuaciones indeterminadas, por ejemplo de la forma

,
Aryabhata I dio una solución, mediante un método que se llamó kuttaka. Brahmagupta estudió y dio soluciones en enteros racionales a las ecuaciones:

A una versión de esta última ecuación Euler le dio crédito a un matemático inglés llamado John Pell, que llamó "ecuación de Pell''. El método de Brahmagupta usado alrededor del 600 d.C. se suele atribuir a Euler (theorema elegantissimum).

Jayadeva en los alrededores del 1 000 dio un método general para resolver ecuaciones de ese tipo. El mismo fue refinado por Bhaskara 100 años despúes. Se parece al "método cíclico inverso'' con fracciones continuas del que se ocuparon muchos matemáticos europeos tiempo después (Fermat,

Euler, Lagrange, Galois).

Es interesante que Bhaskara dio solución a la ecuación 

para x e y mínimos:
x =226153980 e y=1766319049

Este problema fue planteado a manera de reto por Fermat a uno de sus amigos, Frénicle de Bessy en 1 657. Sería resuelto por Lagrange con otro método. Sin embargo, mientras que la solución de Lagrange necesitaba 21 series convergentes sucesivas de la fracción continua de 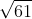de Jayadeva-Bhaskara lo hacía en pocos pasos.

Una de las fuentes de la trigonometría hindú se encuentra en los alejandrinos.

La trigonometría india estaba asociada a la astronomía. Varahamihira las incorpora en su Surya Siddhanta (como en el 400 d.C.) y también lo hace Brahmagupta en Brahma Sputa Siddhanta (como en el 500 d.C.). Pero de manera sistemática lo hace Bhaskara en Siddhanta Siromani.

Los hindúes usaron la semicuerda. Veamos qué quiere decir eso.

Semicuerda hindú

Las funciones que desarrollaron fueron:

Es decir, hay una ligera diferencia con las usuales para nosotros; pero todo se resuelve fácil.
¿Cómo?
Lograron varias relaciones trigonométricas y también desarrollaron tablas de senos de diferentes  arcos. Se afirma que las tablas hindúes tuvieron origen en los babilonios, fuente de la que también  se benefició Ptolomeo.
En el 665, Brahmagupta dio una fórmula de interpolación para calcular los senos de ángulos  intermedios con base en una tabla. Se dice que la fórmula es equivalente a la fórmula de Newton-Stirling para diferencias de segundo orden.
También, un par de siglos después, el astrónomo Govindaswami (alrededor 800 - 850) ofreció una  regla de interpolación de segundo orden para poder calcular valores intermedios de la función, que  se podría considerar era un caso particular de la fórmula de interpolación de Newton-Gauss.
Posteriormente, hubo desarrollos de senos y cosenos con expresiones parecidas a las series de  Taylor para el segundo orden.