Los árabes introdujeron y mejoraron los símbolos del sistema numérico hindú y la notación posicional.
Debe subrayarse que la
cultura científica y matemática bajo dominio musulmán fue
desarrollada por intelectuales provenientes de diferentes pueblos:
persas, judíos, griegos, cristianos, etc., eso sí escrita en árabe.
Sus fuentes en cuanto al
conocimiento griego fueron manuscritos propiamente griegos o
versiones sirias y hebreas. Obtuvieron las obras fundamentales de
Aristóteles, Apolonio, Arquímedes, Diofanto, Herón y las
tradujeron al árabe. Por ejemplo, los Elementos de Euclides fueron
obtenidos de los bizantinos alrededor del año 800 y la obra
astronómica de Ptolomeo, el Almagesto, a la cual ellos dieron
precisamente ese nombre, en el año 827. En realidad se mencionan dos
fuentes:
"Los árabes adquirieron el conocimiento de la ciencia griega a partir de dos fuentes. La mayor parte de ella la aprendieron de los griegos del Imperio bizantino, pero también la adquirieron, de segunda mano, de los cristianos nestorianos de habla siríaca de Persia oriental. Los cristianos nestorianos, desde su centro de Jundishapur, tradujeron durante los siglos VI y VII un importante número de obras griegas científicas -sobre todo de lógica y de medicina- al siríaco, que había reemplazado al griego como lengua culta del Asia occidental desde el siglo III. Después de la conquista árabe, Jundishapur continuó siendo durante un tiempo el primer centro científico y médico del Islam, donde cristianos, judíos y otros súbditos de los califas trabajaban en la traducción de textos del siríaco al árabe. Damasco y Bagdad se convirtieron también en centros de este tipo de trabajo, y ya en el siglo IX se hacían en Bagdad traducciones directas del griego al árabe. En el siglo X casi todos los textos de la ciencia griega que luego se conocieron en Occidente estaban traducidos al árabe.'' [Crombie, A.C.: Historia de la ciencia. De San Agustín a Galileo siglos V-XIII, pp. 44-45]
Los árabes introdujeron
y mejoraron los símbolos del sistema numérico hindú y la notación
posicional. También usaron los irracionales de la misma forma que lo
hicieron los hindúes. Esto debe enfatizarse: Omar Khayyam (1048 -
1122) y Nasir-Eddin (1201 - 1274) afirmaron con toda claridad que las
razones de magnitudes, conmensurables o inconmensurables, podían ser
| Nasir-Eddin |
llamadas números. Resulta interesante, sin embargo, que aunque ellos
conocían el uso de los números negativos y sus reglas de operación,
introducidas por los hindúes, aún así los rechazaron. Con esto ya
tenemos un primer retrato de la cultura islámica. Vamos ahora a
entrar en mayor detalle en las matemáticas.
Se mencionan dos
tradiciones en la astronomía y las matemáticas en Bagdad. Una con
base en las fuentes persas e indias, que subrayaba una aproximación
algebraica en las matemáticas, y también presente en las tablas
astronómicas, y con una motivación práctica. En esa tradición se
coloca al- Khwarizmi. Otra tradición con énfasis en las matemáticas
helenísticas, que subrayaba la geometría y los métodos deductivos.
Su figura emblemática: Tabit ibn Qurra. Ambas tradiciones se
llegarían a fundir, lo que se podrá apreciar en el trabajo de Omar
Khayyam y al-Kashi.
Al-Khwarizmi
Vamos a empezar por Abu Jafar Muhammad ibn Musa al-Khwarizmi (c. 825). Escribió sobre aritmética, álgebra, astronomía y geografía.
Escribió en el 830 el
libro: Hisab Al-jabr w'al-muqabala, que se traduce como Cálculo por
restauración y reducción. También: Algorithmi de numero indorum
(Cálculo con números indios).
Al traducirse al latín
en el siglo XII, el primer libro quedó con el título de Ludus
algebrae et almucgrabalaeque. Y aquí se redujo a álgebra. Este
libro integra las tradiciones babilónicas, griegas e indias.
Los trabajos algebraicos
de al-Khwarizmi se basaron en los resultados de Brahmagupta pero
reflejan, también, influencias babilonias y griegas directamente
(por ejemplo, de Diofanto).
El segundo libro,
Aritmética, sirvió para introducir a los europeos en el sistema
numérico posicional de la India. Incluye un tratamiento sistemático
de las operaciones de la aritmética. Fue el primer libro traducido
del árabe, y hay un detalle interesante: popularizó la palabra
"algoritmo'', que proviene del apellido del autor, para
referirse a procedimientos sistemáticos de cálculo. Y se quedó
para la historia. Se afirma que los números indios llegaron a Bagdad
en el 773 por medio de una misión diplomática hindú.
El documento más antiguo
en Europa con la numeración india se llama Codex Vigilanus y entró por España en el año
976. De hecho, está hoy en un museo de Madrid.
Al-Khwarizmi construyó
tablas astronómicas que tuvieron influencia por 500 años, con base
en las tradiciones babilónicas,
indias y helenísticas.
Su obra Imagen de la
Tierra se considera la más importante de la geografía desde la obra
de Ptolomeo.
Al-Khwarizmi señaló 6
tipos de ecuaciones:
con a,b ,c números
enteros positivos.
Ofreció en todos los
tipos de ecuaciones procedimientos para resolverlas; algunas veces,
dio algún fundamento lógico. Por ejemplo, en el caso del tipo 4,
ofreció el método que normalmente se llama "completar
cuadrados''.
A la par de las
consideraciones algebraicas, al-Khwarizmi buscó su fundamento
téorico en la geometría. Es decir, construía figuras geométricas
para mostrar la evidencia del aserto algebraico. Eso sí, usaba
ejemplos específicos en su demostración.
Ibn Qurra
Abul Hassan Thabit ibn Qurra Marwan al-Harrani hizo trabajos en trigonometría esférica, una prueba del teorema de Pitágoras, medidas de parábolas y paraboloides, y sobre números "amigos''. Se considera el mejor geómetra del mundo islámico.
La generalización del teorema de Pitágoras es un resultado interesante que no se descubrió sino hasta el año 1 953 en Turquía.
La generalización del teorema de Pitágoras es un resultado interesante que no se descubrió sino hasta el año 1 953 en Turquía.
Los ángulos AB'B y AC'C y BCA son iguales por construcción. Entonces:
Aunque no aparece una prueba por ibn Qurra en el texto que se preserva, no es difícil demostrar elresultado usando las propiedades de los triángulos semejantes. ¿Cómo?
Aquí hay un asunto polémico. Se especula que John Wallis pudo haber estado al tanto de este resultado árabe cuando, en el año 1 685, publicó este mismo teorema como suyo en el libro Treatise on angular Sections
A diferencia de al-Khwarizmi, volvemos al uso de la geometría en el álgebra; ibn Qurra hizo una demostración general en la que introdujo dos teoremas de Euclides.
Esta integración de álgebra y geometría, unificaba las dos tradiciones del pensamiento matemático, y abrían el camino al álgebra moderna.
reales, en la tradición de al-Kwarizmi. Ofreció algo parecido al triángulo de Pascal para los coeficientes del binomio. También, intentó una demostración del postulado de las paralelas de Euclides.
Ahora bien, una de sus más importantes contribuciones en la geometría fue una extensión de la teoría de las proporciones de Euclides. Trabajó la dimensión algebraica de esta teoría para extender el concepto de número de tal manera que pudiera incluir a los números irracionales positivos.
En lo que se refiere a la resolución de las cúbicas, usó un método geométrico para resolver ecuaciones de tercer grado con raíces positivas. Estudió 19 tipos de ecuaciones cúbicas, algunas de las cuales las pudo reducir a cuadráticas. Las restantes 14 las resolvió por medio de secciones cónicas. Un ejemplo de esto último:
Consideremos: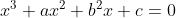 , con a,b,c mayores que 0. Procedamos a usar la sustitución
, con a,b,c mayores que 0. Procedamos a usar la sustitución 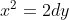 . La ecuación queda:
. La ecuación queda:
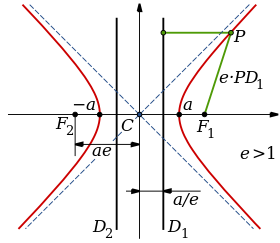
Esta es la ecuación de una hipérbola. Como la ecuación con la que hicimos la sustitución es una parábola, la solución de la cúbica es la intersección de la hipérbola y la parábola.
Debe entenderse, sin embargo, que todo esto se hacía sin el arsenal de simbolismo que posee el álgebra moderna.
La utilización de las secciones cónicas y de la geometría para encontrar soluciones fue el gran aporte de este matemático insigne.
Al-Kashi en la segunda mitad del siglo XIV dio una aproximación para
La contribución árabe a la trigonometría nos la reseña Bell de la siguiente forma:
El interés en la trigonometría por parte de los árabes se vio potenciado cuando entraron en contacto con las tablas de los hindúes. De hecho, la finalidad básica era mejorar la exactitud de éstas. Un ejemplo notable es el de al-Kashi que calculó el valor de 60sen 1° con una exactitud de 16 decimales, usando un método iterativo que aparece en su libro Risala al-watar wa'l-jaib (se traduce
En relación con la geometría, las principales influencias fueron Euclides, Arquímedes y Herón. Fue
Nasir-Eddin quien realizó una sistematización de la trigonometría plana y esférica, la cual no sería conocida por los europeos sino hasta el año 1 450.
Algunos historiadores de las matemáticas opinan que para los árabes las matemáticas no poseían el significado que tenía para los griegos, como parte del objetivo global y edificante de hacer inteligible el mundo, sino, más bien, como un mecanismo para ampliar su dominio sobre la naturaleza. También, se suele afirmar que la contribución árabe se redujo a preservar más que ampliar las matemáticas griegas e hindúes y transmitirlas a Europa.
El influjo de los árabes terminaría en una sucesiva colección de hechos que van desde los ataques de los cruzados, la conquista por los mongoles y la destrucción realizada por los tártaros, y, tiempo después, en España, su derrota por los cristianos.
A pesar de la opinión bastante generalizada de algunos expertos, la realidad es, sin embargo, según demuestran más recientes investigaciones, que los árabes en muchos campos extendieron significativamente el conocimiento recibido de los griegos y los hindúes. No fueron solo compiladores mecánicos del acervo de otra civilización, tampoco fueron un simple puente para el desarrollo de las ciencias en Europa.
Durante siglos, una visión eurocentrista ha dominado buena parte de las opiniones sobre el desarrollo cultural y científico de la humanidad, en particular, con una subestimación de las contribuciones de pueblos ajenos a Europa occidental. El caso de los árabes es uno de ellos. Afortunadamente, en los últimos tiempos hay una revalorización que ha permitido visualizar la historia de Occidente de una manera diferente, en particular de las ciencias y las matemáticas.
Algunos de los elementos que en las matemáticas son indiscutiblemente construcciones diferentes de las griegas, son, para empezar, la notación posicional en base 10, el uso de números negativos y de números irracionales, afirmados explícitamente como números, un álgebra con letras y operaciones.
Los resultados hindúes y árabes permitieron construir un fundamento más avanzado para el álgebra que el que se tuvo en la Antigüedad Griega. Por ejemplo, con el uso de símbolos de una manera más sistemática, una profundización en el estudio de las ecuaciones indeterminadas, en las ecuaciones de tercer grado, y, sin duda, un progreso en la trigonometría.
Se debe subrayar, además, que, los árabes, al aceptar el uso de los números irracionales de una manera extensiva hacían posible dar valores numéricos a los segmentos de recta y a todas aquellas figuras geométricas que en la Antigüedad Griega tuvieron que ser limitadas a magnitudes cualitativas.
La práctica de resolver ecuaciones algebraicas por un lado y luego, por el otro, realizar justificaciones geométricas, un "paralelismo'' de estas dos disciplinas, se debe interpretar como un valioso fundamento para lo que luego se llamaría la geometría analítica.
Aquí, por último, es necesario hacer un comentario general. Tanto los hindúes como los árabes utilizaron la aritmética y el álgebra sin prestar demasiado cuidado a las demostraciones deductivas como los griegos en la geometría. Los árabes eran conscientes de estas características de la matemática griega y estaban plenamente familiarizados con los requerimientos de la demostración axiomática. Sin embargo, privilegiaron la aproximación práctica presente en la aritmética, el álgebra, y en la formulación algebraica de las relaciones trigonométricas. Es decir, el énfasis en estas disciplinas, carentes de la demostración axiomática y deductiva de la geometría sintética, revela una visión, ideología y actitud diferentes en estas civilizaciones, más orientadas hacia necesidades prácticas que requieren un tratamiento cuantitativo, y que se proporciona mejor con la aritmética y el álgebra. Aunque los árabes y los hindúes eran conscientes, hasta cierto punto, de esta ausencia de fundamentos lógicos en la aritmética y el álgebra, enfatizaron estas disciplinas a través de la intuición y la heurística, dejando para luego las correcciones y justificaciones lógicas. Esto permitió un gran desarrollo del álgebra y la aritmética, lo que sería un componente esencial para los desarrollos científicos y matemáticos de Europa occidental.
Dos tradiciones se heredaron en las matemáticas occidentales. Por un lado, los objetos y métodos de la geometría clásica griega, con sus virtudes y sus debilidades, y, por el otro lado, esta tradición cultural y científica que retomó las contribuciones egipcias y babilonias, algunos resultados de los matemáticos alejandrinos en la aritmética y el álgebra, y los desarrollos en estos campos de los hindúes y los árabes. Esto dos componentes desarrollarían una dialéctica y encontrarían una magnífica síntesis en las mismas culturas islámicas, pero en el mundo europeo, con precisión, en la geometría analítica y, posteriormente, en el cálculo diferencial e integral.
Aunque no aparece una prueba por ibn Qurra en el texto que se preserva, no es difícil demostrar elresultado usando las propiedades de los triángulos semejantes. ¿Cómo?
Aquí hay un asunto polémico. Se especula que John Wallis pudo haber estado al tanto de este resultado árabe cuando, en el año 1 685, publicó este mismo teorema como suyo en el libro Treatise on angular Sections
 | |
| Treatise on angular Sections de John Wallis |
A diferencia de al-Khwarizmi, volvemos al uso de la geometría en el álgebra; ibn Qurra hizo una demostración general en la que introdujo dos teoremas de Euclides.
Esta integración de álgebra y geometría, unificaba las dos tradiciones del pensamiento matemático, y abrían el camino al álgebra moderna.
Omar Khayyam
Existe consenso entre los historiadores de las matemáticas en que la figura en este terreno más importante fue Abdul-Fath Umar ibn Ibrahim al-Kayyami, Omar Khayyam. Dio reglas para resolver ecuaciones cuadráticas y un método para la resolución de ecuaciones cúbicas con raíces
reales, en la tradición de al-Kwarizmi. Ofreció algo parecido al triángulo de Pascal para los coeficientes del binomio. También, intentó una demostración del postulado de las paralelas de Euclides.
Ahora bien, una de sus más importantes contribuciones en la geometría fue una extensión de la teoría de las proporciones de Euclides. Trabajó la dimensión algebraica de esta teoría para extender el concepto de número de tal manera que pudiera incluir a los números irracionales positivos.
En lo que se refiere a la resolución de las cúbicas, usó un método geométrico para resolver ecuaciones de tercer grado con raíces positivas. Estudió 19 tipos de ecuaciones cúbicas, algunas de las cuales las pudo reducir a cuadráticas. Las restantes 14 las resolvió por medio de secciones cónicas. Un ejemplo de esto último:
Consideremos:
Esta es la ecuación de una hipérbola. Como la ecuación con la que hicimos la sustitución es una parábola, la solución de la cúbica es la intersección de la hipérbola y la parábola.
Debe entenderse, sin embargo, que todo esto se hacía sin el arsenal de simbolismo que posee el álgebra moderna.
La utilización de las secciones cónicas y de la geometría para encontrar soluciones fue el gran aporte de este matemático insigne.
Otros resultados
 |
Al-Kashi |
Al-Kashi en la segunda mitad del siglo XIV dio una aproximación para  con 16 decimales correctos por medio de circunscribir en un círculo un polígono con 3x228 lados. Su libro Miftah al-hisab, 1 427, se dice que es uno de los mejores compendios de la aritmética y el álgebra árabes hasta su tiempo. En esta La clave del calculista hace un tratamiento completo de los métodos aritméticos, incluso con fracciones decimales.
con 16 decimales correctos por medio de circunscribir en un círculo un polígono con 3x228 lados. Su libro Miftah al-hisab, 1 427, se dice que es uno de los mejores compendios de la aritmética y el álgebra árabes hasta su tiempo. En esta La clave del calculista hace un tratamiento completo de los métodos aritméticos, incluso con fracciones decimales.
Las fracciones decimales habían aparecido por primera vez en una obra de Abul Hassan al-Uqlidisi del año 952 o 953: El libro de los capítulos sobre la aritmética india. Este conocía el método para multiplicarlas por enteros. Sin embargo, al-Kashi en el siglo XV dio el tratamiento completo a las operaciones con decimales.
Trigonometría
| Al-Battani |
"Los árabes adoptaron y desarrollaron la trigonometría hindú. El primer progreso notable se debió al astrónomo Al-Battani (muerto en el 929), en el siglo IX. Si bien en realidad no fue el primero que aplicó el álgebra en lugar de la sola geometría a la trigonometría, este astrónomo matemático fue el primero que dio un gran paso en esa dirección. Usó además del seno hindú, la tangente y la cotangente. En el siglo X se calcularon tablas de estas dos últimas, y también hicieron su aparición la secante y la cosecante como razones trigonométricas. Por estar el concepto de función todavía unos 600 años en el futuro, nada en su obra se parece mucho a la trigonometría elemental de hoy día.'' [Bell, E.T.: Historia de las matemáticas, p. 112.]
De hecho, la función seno fue traída de la matemática india se supone que a través de un texto de astronomía india Surya Siddhanta. También rsen α y r-rsen α fueron incorporadas de los hindúes . Las funciones tangente y cotangente sí son de origen árabe
Abul Wafa había realizado un estudio sistemático de las 6 funciones trigonométricas, y en particular dio las relaciones:
El interés en la trigonometría por parte de los árabes se vio potenciado cuando entraron en contacto con las tablas de los hindúes. De hecho, la finalidad básica era mejorar la exactitud de éstas. Un ejemplo notable es el de al-Kashi que calculó el valor de 60sen 1° con una exactitud de 16 decimales, usando un método iterativo que aparece en su libro Risala al-watar wa'l-jaib (se traduce
como Tratado sobre la cuerda y el seno), y que suponía la resolución de ecuaciones de tercer grado.
Un balance
Es importante poner énfasis en la relación privilegiada entre árabes y griegos, por ejemplo, en su resolución de ecuaciones algebraicas cuadráticas. A pesar de la perspectiva más aritmética y algebraica de los hindúes, con la cual estaban familiarizado los árabes, al-Khwarizmi introducía justificaciones geométricas. Está claro: asumieron en cierta forma la influencia griega.En relación con la geometría, las principales influencias fueron Euclides, Arquímedes y Herón. Fue
Nasir-Eddin quien realizó una sistematización de la trigonometría plana y esférica, la cual no sería conocida por los europeos sino hasta el año 1 450.
Algunos historiadores de las matemáticas opinan que para los árabes las matemáticas no poseían el significado que tenía para los griegos, como parte del objetivo global y edificante de hacer inteligible el mundo, sino, más bien, como un mecanismo para ampliar su dominio sobre la naturaleza. También, se suele afirmar que la contribución árabe se redujo a preservar más que ampliar las matemáticas griegas e hindúes y transmitirlas a Europa.
El influjo de los árabes terminaría en una sucesiva colección de hechos que van desde los ataques de los cruzados, la conquista por los mongoles y la destrucción realizada por los tártaros, y, tiempo después, en España, su derrota por los cristianos.
A pesar de la opinión bastante generalizada de algunos expertos, la realidad es, sin embargo, según demuestran más recientes investigaciones, que los árabes en muchos campos extendieron significativamente el conocimiento recibido de los griegos y los hindúes. No fueron solo compiladores mecánicos del acervo de otra civilización, tampoco fueron un simple puente para el desarrollo de las ciencias en Europa.
Durante siglos, una visión eurocentrista ha dominado buena parte de las opiniones sobre el desarrollo cultural y científico de la humanidad, en particular, con una subestimación de las contribuciones de pueblos ajenos a Europa occidental. El caso de los árabes es uno de ellos. Afortunadamente, en los últimos tiempos hay una revalorización que ha permitido visualizar la historia de Occidente de una manera diferente, en particular de las ciencias y las matemáticas.
Algunos de los elementos que en las matemáticas son indiscutiblemente construcciones diferentes de las griegas, son, para empezar, la notación posicional en base 10, el uso de números negativos y de números irracionales, afirmados explícitamente como números, un álgebra con letras y operaciones.
Los resultados hindúes y árabes permitieron construir un fundamento más avanzado para el álgebra que el que se tuvo en la Antigüedad Griega. Por ejemplo, con el uso de símbolos de una manera más sistemática, una profundización en el estudio de las ecuaciones indeterminadas, en las ecuaciones de tercer grado, y, sin duda, un progreso en la trigonometría.
Se debe subrayar, además, que, los árabes, al aceptar el uso de los números irracionales de una manera extensiva hacían posible dar valores numéricos a los segmentos de recta y a todas aquellas figuras geométricas que en la Antigüedad Griega tuvieron que ser limitadas a magnitudes cualitativas.
La práctica de resolver ecuaciones algebraicas por un lado y luego, por el otro, realizar justificaciones geométricas, un "paralelismo'' de estas dos disciplinas, se debe interpretar como un valioso fundamento para lo que luego se llamaría la geometría analítica.
Aquí, por último, es necesario hacer un comentario general. Tanto los hindúes como los árabes utilizaron la aritmética y el álgebra sin prestar demasiado cuidado a las demostraciones deductivas como los griegos en la geometría. Los árabes eran conscientes de estas características de la matemática griega y estaban plenamente familiarizados con los requerimientos de la demostración axiomática. Sin embargo, privilegiaron la aproximación práctica presente en la aritmética, el álgebra, y en la formulación algebraica de las relaciones trigonométricas. Es decir, el énfasis en estas disciplinas, carentes de la demostración axiomática y deductiva de la geometría sintética, revela una visión, ideología y actitud diferentes en estas civilizaciones, más orientadas hacia necesidades prácticas que requieren un tratamiento cuantitativo, y que se proporciona mejor con la aritmética y el álgebra. Aunque los árabes y los hindúes eran conscientes, hasta cierto punto, de esta ausencia de fundamentos lógicos en la aritmética y el álgebra, enfatizaron estas disciplinas a través de la intuición y la heurística, dejando para luego las correcciones y justificaciones lógicas. Esto permitió un gran desarrollo del álgebra y la aritmética, lo que sería un componente esencial para los desarrollos científicos y matemáticos de Europa occidental.
Dos tradiciones se heredaron en las matemáticas occidentales. Por un lado, los objetos y métodos de la geometría clásica griega, con sus virtudes y sus debilidades, y, por el otro lado, esta tradición cultural y científica que retomó las contribuciones egipcias y babilonias, algunos resultados de los matemáticos alejandrinos en la aritmética y el álgebra, y los desarrollos en estos campos de los hindúes y los árabes. Esto dos componentes desarrollarían una dialéctica y encontrarían una magnífica síntesis en las mismas culturas islámicas, pero en el mundo europeo, con precisión, en la geometría analítica y, posteriormente, en el cálculo diferencial e integral.










No hay comentarios:
Publicar un comentario